题目内容
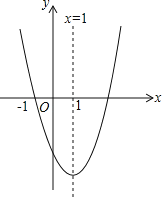
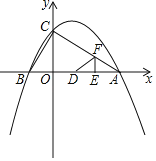
【题目】如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)
(1)求此二次函数的解析式及顶点坐标.
(2)设点P是该抛物线上的动点,当△ABP的面积等于△ABC面积的![]() 时,求出点P的坐标.
时,求出点P的坐标.
【答案】(1)y=x2+2x﹣3,顶点坐标(﹣1,﹣4);(2)P点坐标为(﹣4,5),(2,5).
【解析】
(1)将点A、C的坐标分别代入函数解析式,列出关于b、c的方程组,通过解方程组求得它们的值即可;
(2)根据抛物线与坐标轴交点的求法求得点B的坐标,结合三角形的面积公式求得△ABC的面积=6,进而求得△ABP的面积=10,根据△ABP的面积可以计算出点P的纵坐标的值,然后再利用二次函数解析式计算出点P的横坐标即可.
解:(1)根据题意得:![]() .
.
解得:b=2,c=﹣3,
∴二次函数的解析式为y=x2+2x﹣3,
∵y=x2+2x﹣3=(x+1)2﹣4;
∴顶点坐标(﹣1,﹣4);
(2)当y=0时,x2+2x﹣3=0,解得x1=﹣3,x2=1,则B(﹣3,0),A(1,0),
∴AB=4
∵C(0,﹣3)
∴△ABC的面积=![]() ×4×3=6,
×4×3=6,
∵△ABP的面积等于△ABC面积的![]()
∴△ABP的面积=![]() ×6=10,
×6=10,
∴![]() 4×|yp|=10
4×|yp|=10
∴|yp|=5,
∴yp=±5,
当yp=5时 解方程x2+2x﹣3=5得x1=﹣4,x2=2,此时P点坐标为(﹣4,5),(2,5);
当yp=﹣5时,方程x2+2x﹣3=﹣5没有实数解,
∴P点坐标为(﹣4,5),(2,5).

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目