题目内容
 如图在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若
如图在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若| AD |
| BD |
| 1 |
| 3 |
8
8
.分析:根据
=
,可得
=
,再由DE∥BC,可判断△ADE∽△ABC,利用对应边成比例可得出BC的长.
| AD |
| BD |
| 1 |
| 3 |
| AD |
| AB |
| 1 |
| 4 |
解答:解:∵
=
,
∴
=
,
∵DE∥BC,
∴△ADE∽△ABC,
∴
=
=
,
又∵DE=2,
∴BC=8.
故答案为:8.
| AD |
| BD |
| 1 |
| 3 |
∴
| AD |
| AB |
| 1 |
| 4 |
∵DE∥BC,
∴△ADE∽△ABC,
∴
| DE |
| BC |
| AD |
| AB |
| 1 |
| 4 |
又∵DE=2,
∴BC=8.
故答案为:8.
点评:本题考查了相似三角形的判定与性质,解答本题的关键是掌握相似三角形的对应边成比例.

练习册系列答案
相关题目
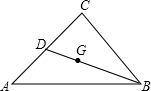 如图在△ABC中,点G是重心,连接BG并延长BG交AC于D,若点G到AB的距离为2,则点D到AB的距离是( )
如图在△ABC中,点G是重心,连接BG并延长BG交AC于D,若点G到AB的距离为2,则点D到AB的距离是( )| A、2.5 | B、3 | C、3.6 | D、4 |
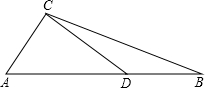 如图在△ABC中,点D是AB的中点,DC⊥AC,且tan∠BCD=
如图在△ABC中,点D是AB的中点,DC⊥AC,且tan∠BCD=

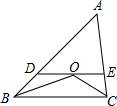 如图在△ABC中,点O是∠ABC与∠ACB的平分线的交点,过点O作DE∥BC,交AB于D,交AC于E,若BD=4,CE=3,则DE=
如图在△ABC中,点O是∠ABC与∠ACB的平分线的交点,过点O作DE∥BC,交AB于D,交AC于E,若BD=4,CE=3,则DE=