题目内容
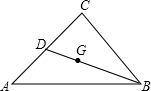如图在△ABC中，点G是重心，连接BG并延长BG交AC于D，若点G到AB的距离为2，则点D到AB的距离是（ ）| A、2.5 | B、3 | C、3.6 | D、4 |
分析：分别过D，G作GE⊥AB，DF⊥AB，根据相似三角形的判定可得到△BGE∽△BDF，再根据相似三角形对应边的比等于相似比，从而不难求得DF的长．
解答：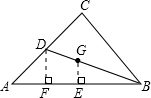
解：分别过D，G作GE⊥AB，DF⊥AB，
∵点G是△ABC的重心
∴BG=2DG
设DG=x，则GB=2x
∵GE⊥AB，DF⊥AB，∠ABD=∠ABD
∴△BGE∽△BDF
∴
=
即
=
∴DF=3．
故选B．
解：分别过D，G作GE⊥AB，DF⊥AB，∵点G是△ABC的重心
∴BG=2DG
设DG=x，则GB=2x
∵GE⊥AB，DF⊥AB，∠ABD=∠ABD
∴△BGE∽△BDF
∴
| BG |
| BG+GD |
| GE |
| DF |
即
| 2x |
| 3x |
| 2 |
| DF |
∴DF=3．
故选B．
点评：解答此题要熟知三角形重心的概念及性质：三角形的重心是三角形三边中线的交点，重心分中线为2：1．
练习册系列答案
相关题目
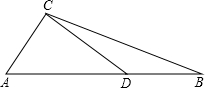如图在△ABC中，点D是AB的中点，DC⊥AC，且tan∠BCD=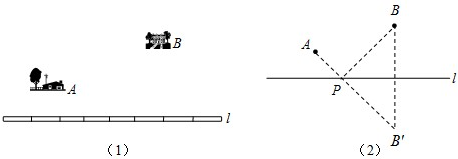
如图在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若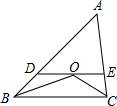
如图在△ABC中，点O是∠ABC与∠ACB的平分线的交点，过点O作DE∥BC，交AB于D，交AC于E，若BD=4，CE=3，则DE=