题目内容
 如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为________.
如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为________.
9
分析:过P分别作x轴和y轴的垂线,交x轴和y轴与C和D.构造全等三角形△PDB≌△PCA(ASA)、正方形CODP;所以S四边形OAPB=S正方形ODPC=3×3=9.
解答: 解:过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D.
解:过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D.
∵P点坐标为(3,3),
∴PC=PD;
又∵l1⊥l2,
∴∠BPA=90°;
又∵∠DPC=90°,
∴∠DPB=∠PCA,
△PDB≌△PCA(ASA),
∴S△DPB=S△PCA,
S四边形OAPB=S正方形ODPC+S△PCA-S△DPB,
即S四边形OAPB=S正方形ODPC=3×3=9.
故答案是:9.
点评:本题综合考查了垂线、坐标与图形性质、三角形的面积.解答此题时,利用了“割补法”求四边形OAPB的面积.
分析:过P分别作x轴和y轴的垂线,交x轴和y轴与C和D.构造全等三角形△PDB≌△PCA(ASA)、正方形CODP;所以S四边形OAPB=S正方形ODPC=3×3=9.
解答:
 解:过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D.
解:过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D.∵P点坐标为(3,3),
∴PC=PD;
又∵l1⊥l2,
∴∠BPA=90°;
又∵∠DPC=90°,
∴∠DPB=∠PCA,
△PDB≌△PCA(ASA),
∴S△DPB=S△PCA,
S四边形OAPB=S正方形ODPC+S△PCA-S△DPB,
即S四边形OAPB=S正方形ODPC=3×3=9.
故答案是:9.
点评:本题综合考查了垂线、坐标与图形性质、三角形的面积.解答此题时,利用了“割补法”求四边形OAPB的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
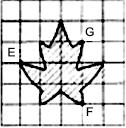 19、如图,若点E坐标为(-2,1),点F坐标为(1,-1),则点G的坐标为
19、如图,若点E坐标为(-2,1),点F坐标为(1,-1),则点G的坐标为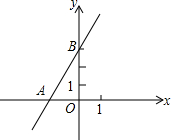 (2012•西城区一模)已知:如图,A点坐标为
(2012•西城区一模)已知:如图,A点坐标为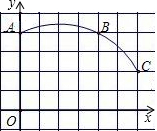 如图,B点坐标为(4,4),则该弧所在圆心的坐标是
如图,B点坐标为(4,4),则该弧所在圆心的坐标是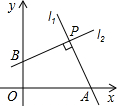 如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为
如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为 如图,A点坐标为(2,2),B点坐标为(2,0).
如图,A点坐标为(2,2),B点坐标为(2,0).