��Ŀ����
����Ŀ������ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ![]() ��
��![]() ��
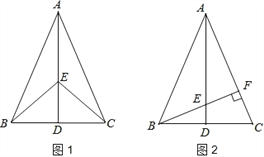
��![]() ������������ε������С��ͬѧ�ڽ�������ʱ���Ȼ�һ������������ÿ��С�����εı߳�Ϊ1�������������л��������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ��������������ABC�ĸߣ�������������ܼ����������������ַ���������ͼ����
������������ε������С��ͬѧ�ڽ�������ʱ���Ȼ�һ������������ÿ��С�����εı߳�Ϊ1�������������л��������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ��������������ABC�ĸߣ�������������ܼ����������������ַ���������ͼ����
��1����ABC��������� ����
��2������DEF���ߵij��ֱ�Ϊ![]() ��
��![]() ��
��![]() ������ͼ2�������������л�����Ӧ����DEF�������ù�ͼ������������Ϊ�� ����
������ͼ2�������������л�����Ӧ����DEF�������ù�ͼ������������Ϊ�� ����
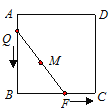
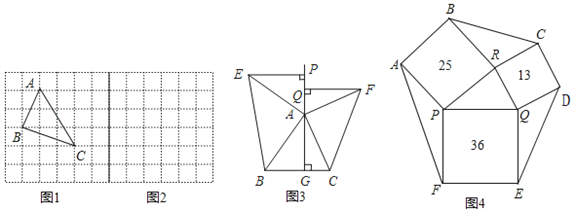
��3����ͼ3����ABC�У�AG��BC�ڵ�G����AΪֱ�Ƕ��㣬�ֱ���AB��ACΪֱ�DZߣ�����ABC��������Rt��ABE�͵���Rt��ACF������E��F������GA�Ĵ��ߣ�����ֱ�ΪP��Q����̽��EP��FQ֮���������ϵ����֤����Ľ��ۣ�
��4����ͼ4��һ�������εĻ�̳���ָ��7�����֣�����������PRBA��RQDC��QPFE������ֱ�Ϊ13m2��25m2��36m2���������λ�̳ABCDEF��������� ��m2��
���𰸡���1��3.5����2��3�� ��3��EP=FQ��֤������������4��110m��
����������������1�����á�ABC���ڵ������ε������ȥ��������Сֱ�������ε���������㼴�ɵý⣻
��2����������ṹ���ɶ���������DEF�������á�DEF���ڵľ��ε������ȥ��������Сֱ�������ε���������㼴�ɵý⣻��3������ͬ�ǵ������������BAG=��AEP��Ȼ�����á��ǽDZߡ�֤����ABG�͡�EAPȫ�ȣ�ͬ����֤��ACG�͡�FAQȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�EP=AG=FQ����4����R��RH��PQ��H����PH=h����Rt��PRH��Rt��RQH�У����ù��ɶ�����ʽ��ʾ��PQ��Ȼ��������������h���Ӷ������PQR��������ٸ��������α��ֳɵ��ĸ������ε������ȣ���������ڸ����ֵ����֮����ʽ���㼴�ɵý⣮
���������
(1)��ABC�����=3��3![]() ��2��1
��2��1![]() ��3��1
��3��1![]() ��2��3=911.53=95.5=3.5��
��2��3=911.53=95.5=3.5��
(2)��DEF��ͼ2��ʾ:

���=2��4![]() ��1��2
��1��2![]() ��2��2
��2��2![]() ��1��4=8122=85=3��
��1��4=8122=85=3��
(3) EP=FQ��
֤�����ߡ�ABE�ǵ���ֱ�������Σ���AB=AE,��BAE=90��
���PAE+��BAG=180��90��=90��,�֡ߡ�AEP+��PAE=90�㣬���BAG=��AEP��
�ڡ�ABG�͡�EAP�У�
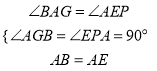 �����ABG�ա�EAP(AAS)��ͬ����֤,��ACG�ա�FAQ����EP=AG=FQ��
�����ABG�ա�EAP(AAS)��ͬ����֤,��ACG�ա�FAQ����EP=AG=FQ��
(4)��ͼ4����R��RH��PQ��H����RH=h��

��Rt��PRH��,PH=![]() ��
��
��Rt��RQH��,QH=![]() ,
,
��PQ=![]() =6��
=6��
![]() ��
��
����ƽ����,25h=3612![]() +13h��
+13h��
������, ![]() =2��
=2��
����ƽ����,13h=4��
���h=3��
��![]() ��6��3=9��
��6��3=9��
�������λ�̳ABCDEF�����=25+13+36+4��9=74+36=110m.

����Ŀ��Ϊ�˽�����õ����,С����С������������30����ͥ�����õ���,������±�:
���õ���/�� | 40 | 50 | 60 | 80 | 90 | 100 |
���� | 6 | 7 | 9 | 5 | 2 | 1 |
����30����ͥ�����õ�������������λ���ֱ��� ( )
A. 60��60 B. 60��50 C. 50��60 D. 50��70