题目内容
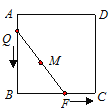
【题目】如图,正方形ABCD的边长为2,将长为2的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到点A为止,同时点F从点B出发,沿图中所示方向按B→C→D→A→B滑动到点B为止,那么在这个过程中,线段QF的中点M所经过的路线围成的图形的面积为 .
【答案】4-π
【解析】根据题意得点M到正方形各顶点的距离都为2,点M所走的运动轨迹为以正方形各顶点为圆心,以2为半径的四个扇形,
∴点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积。
而正方形ABCD的面积为4×4=16,4个扇形的面积为![]() =4π,
=4π,
∴点M所经过的路线围成的图形的面积为164π.
故答案为164π
点睛: 根据直角三角形的性质,斜边上的中线等于斜边的一半,可知:点M到正方形各顶点的距离都为2,故点M所走的运动轨迹为以正方形各顶点为圆心,以2为半径的四个扇形,点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积.

练习册系列答案
相关题目