题目内容
（1）若单独投资A种产品，则所获利润yA（万元）与投资金额x（万元）之间满足正比例函数关系：yA=kx；
（2）若单独投资B种产品，则所获利润yB（万元）与投资金额x（万元）之间满足二次函数关系：yB=ax2+bx．
（3）根据公司信息部的报告，yA，yB（万元）与投资金额x（万元）的部分对应值如下表所示：
| x | 1 | 5 |
| yA | 0.8 | 4 |
| yB | 3.8 | 15 |
（2）若公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为W（万元），试写出W与某种产品的投资金额t（万元）之间的函数关系式；
（3）请你设计一个在（2）中能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少万元？
（2）设投资x万元生产B产品，则投资（20-x）万元生产A产品求出w与x的函数关系式．
（3）把w与x的函数关系式用配方法化简可解出此方案能获得的最大利润是多少万元．
yA=0.8x，yB=-0.2x2+4x
（2）设投资x万元生产B产品，则投资（20-x）万元生产A产品，则
W=0.8（20-x）-0.2x2+4x
=-0.2x2+3.2x+16；
（3）∵w=-0.2x2+3.2x+16=-0.2（x-8）2+28.8
∴投资8万元生产B产品，12万元生产A产品可获得最大利润28.8万元．
故答案为：0.8x，-0.2x2+4x
每课必练系列答案
巧学巧练系列答案| 4 |
| 5 |
| x | 1 | 5 |
| y2 | 3.8 | 15 |
（2）如果公司准备投资10万元同时开发甲、乙两种新产品，设公司所获得的总利润为P（万元），试写出P与乙种产品的投资金额x之间的函数关系式，并求出获得最大利润的投资方案．
某公司准备投资开发A、B两种新产品，通过市场调研发现：如果单独投资A种产品，则所获利润（万元）与投资金额
（万元）之间满足正比例函数关系：
；如果单独投资B种产品，则所获利润（万元）与投资金额（万元）之间满足二次函数关系：
．根据公司信息部的报告，
，
（万元）与投资金额（万元）的部分对应值如下表所示：
|
| 1 | 5 |
|
| 0．8 | 4 |
|
| 3．8 | 15 |
1.填空：
；
；
2.如果公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为w（万元），试写出w与某种产品的投资金额x之间的函数关系式；
3.请你设计一个在⑵中能获得最大利润的投资方案．
某公司准备投资开发A、B两种新产品，通过市场调研发现：如果单独投资A种产品，则所获利润（万元）与投资金额（万元）之间满足正比例函数关系：
；如果单独投资B种产品，则所获利润（万元）与投资金额
（万元）之间满足二次函数关系：
．根据公司信息部的报告，
，
（万元）与投资金额
（万元）的部分对应值如下表所示：
| | 1 | 5 |
| | 0．8 | 4 |
| | 3．8 | 15 |
（1）填空： ；
；
（2）如果公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为w（万元），试写出w与某种产品的投资金额x之间的函数关系式；
（3）请你设计一个在⑵中能获得最大利润的投资方案．
某公司准备投资开发A、B两种新产品，通过市场调研发现：如果单独投资A种产品，则所获利润（万元）与投资金额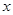
（万元）之间满足正比例函数关系：
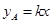；如果单独投资B种产品，则所获利润（万元）与投资金额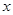（万元）之间满足二次函数关系：
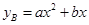．根据公司信息部的报告，
，
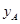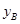（万元）与投资金额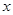（万元）的部分对应值如下表所示：
|
|
1 |
5 |
|
|
0．8 |
4 |
|
|
3．8 |
15 |
（1）填空：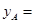
；
；
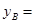（2）如果公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为w（万元），试写出w与某种产品的投资金额x之间的函数关系式；
（3）请你设计一个在⑵中能获得最大利润的投资方案．