题目内容
24、实践与探索!
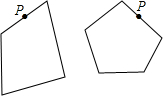
①过四边形一边上点P与另外两个顶点连线可以把四边形分成
②过五边形一边上点P与另外三个顶点连线可以把五边形分成
③经过上面的探究,你可以归纳出过n边形一边上点P与另外
④你能否根据这样划分多边形的方法来写出n边形的内角和公式?请说明你的理由.
①过四边形一边上点P与另外两个顶点连线可以把四边形分成
3
个三角形;②过五边形一边上点P与另外三个顶点连线可以把五边形分成
4
个三角形;③经过上面的探究,你可以归纳出过n边形一边上点P与另外
n-2
个顶点连线可以把n边形分成n-1
个三角形(用含n的代数式表示).④你能否根据这样划分多边形的方法来写出n边形的内角和公式?请说明你的理由.

分析:①②③在n边形的边上任意取一点,连接这点与各顶点的线段可以把n边形分成(n-1)个三角形;
④欲证明多边形的内角和定理,可以把多边形的内角转移到三角形中,利用(n-1)个三角形,内角和为(n-1)×180°,n边形的内角和还要再减去P所在的一个平角,所以n边形的内角和为(n-2)×180°.
④欲证明多边形的内角和定理,可以把多边形的内角转移到三角形中,利用(n-1)个三角形,内角和为(n-1)×180°,n边形的内角和还要再减去P所在的一个平角,所以n边形的内角和为(n-2)×180°.
解答:解:①过四边形一边上点P与另外两个顶点连线可以把四边形分成4-1=3个三角形;
②过五边形一边上点P与另外三个顶点连线可以把五边形分成5-1=4个三角形;
③经过上面的探究,你可以归纳出过n边形一边上点P与另外(n-2)个顶点连线可以把n边形分成 (n-2)个三角形(用含n的代数式表示).
④在n边形的任意一边上任取一点P,连接P点与其它各顶点的线段可以把n边形分成(n-1)个三角形,
这(n-1)个三角形的内角和等于(n-1)•180°,
以P为公共顶点的(n-1)个角的和是180°,
所以n边形的内角和是(n-1)•180°-180°=(n-2)•180°.
故答案为:3;4;n-2,n-1.
②过五边形一边上点P与另外三个顶点连线可以把五边形分成5-1=4个三角形;
③经过上面的探究,你可以归纳出过n边形一边上点P与另外(n-2)个顶点连线可以把n边形分成 (n-2)个三角形(用含n的代数式表示).
④在n边形的任意一边上任取一点P,连接P点与其它各顶点的线段可以把n边形分成(n-1)个三角形,
这(n-1)个三角形的内角和等于(n-1)•180°,
以P为公共顶点的(n-1)个角的和是180°,
所以n边形的内角和是(n-1)•180°-180°=(n-2)•180°.
故答案为:3;4;n-2,n-1.
点评:本题考查了多边形的内角和定理的证明,解题关键是将多边形的内角和问题转化为三角形中解决,在n边形的任意一边上任取一点P,连接P点与其它各顶点的线段可以把n边形分成(n-1)个三角形.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

 实践与探索!
实践与探索!