��Ŀ����
��֪��ͼ����ƽ��ֱ������ϵ�����ĵ㣬����ֱ�ΪA��-4��3����B��4��3����M��0��1����Q��1��2��������P���߶�AB�ϣ��ӵ�A�������B��ÿ��1����λ�˶�������PM��PQ���ӳ��ֱ�x����C��D���㣨��ͼ������1���ڵ�P�ƶ��Ĺ����У�����M��C��D��Q��Χ���ı��Σ���t��ȡֵ��Χ��
��2���ڵ�P�ƶ��Ĺ����У���PMQ��������Գ�ͼ�������ܣ���������������ĵ�P�����ꣻ�����ܣ���˵�����ɣ�
��3���ڵ�P�ƶ��Ĺ����У����ı���MCDQ�����S�ķ�Χ��
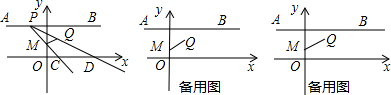
��������1�������ֱ��AB��y��Ľ���ΪR�Ļ������ҪʹM��Q��D��C�ܹ����ı��Σ���ôP������߶�AB���˶����Ҳ���ֱ��QM�ϣ��ɴ˿����t��ȡֵ��Χ����t=2ʱ��PR=2������MR��OM=2��1���ɵó�OC=1����C��1��0����
��2�������PMQ����Գ�ͼ�Σ���ô��PMQ��Ϊ���������Σ�Ӧ����������������P�㣺
��P��MQ�Ĵ�ֱƽ�����ϣ������P������꣬Ȼ��������ϵ�����ľ��빫ʽ��ʾ��PQ��PM�����ڴ�ʱPQ=PM���ݴ˿����P�����ꣻ
�ڸ���Q��M�������֪���������RQ����ô������MQR�ǵ���ֱ�������Σ����R�㼴��0��3��Ҳ��������������PQ=QMʱ����ֱ��AB�ϣ�����һ�㣬�����ǵ���ֱ��QM�ϣ���˲���������ȥ����
��3������ֻ�����S�����ֵ���ɣ�������������ۣ�
�ٵ�0��t��4ʱ����Q��QM��x����N����ʱ�ı���MCQD�������������MQNO�����+������QND�����-������MOC�������ã��ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
�ڵ�4��t��5ʱ���������������MOQN�����+������MCO�����+������QND�������ã�
�۵�5��t��8��t��6��ʱ������������ı���������QNC�����-����MONQ�����-������MOD�������ã�
����������������ó��ĺ�����ϵʽ�����Ե��Ա���ȡֵ��Χ�������S�����ֵ�����ɵó�S��ȡֵ��Χ��
��2�������PMQ����Գ�ͼ�Σ���ô��PMQ��Ϊ���������Σ�Ӧ����������������P�㣺
��P��MQ�Ĵ�ֱƽ�����ϣ������P������꣬Ȼ��������ϵ�����ľ��빫ʽ��ʾ��PQ��PM�����ڴ�ʱPQ=PM���ݴ˿����P�����ꣻ
�ڸ���Q��M�������֪���������RQ����ô������MQR�ǵ���ֱ�������Σ����R�㼴��0��3��Ҳ��������������PQ=QMʱ����ֱ��AB�ϣ�����һ�㣬�����ǵ���ֱ��QM�ϣ���˲���������ȥ����
��3������ֻ�����S�����ֵ���ɣ�������������ۣ�
�ٵ�0��t��4ʱ����Q��QM��x����N����ʱ�ı���MCQD�������������MQNO�����+������QND�����-������MOC�������ã��ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
�ڵ�4��t��5ʱ���������������MOQN�����+������MCO�����+������QND�������ã�
�۵�5��t��8��t��6��ʱ������������ı���������QNC�����-����MONQ�����-������MOD�������ã�
����������������ó��ĺ�����ϵʽ�����Ե��Ա���ȡֵ��Χ�������S�����ֵ�����ɵó�S��ȡֵ��Χ��
����⣺��1��0��t��8����t��6����C������Ϊ��1��0����
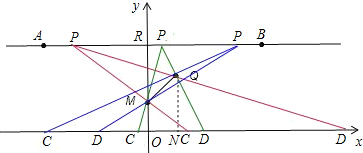
��2������PMQ��������Գ�ͼ�Σ����PMQ��Ϊ���������Σ�
�ٵ�PQ=PMʱ����P������ΪP��a��3�������У�
PQ=
=
��
��֪MQ=
��
��
=
��
���a=2��a=0��
��a=2ʱ��AP=4+2=6����t=6�������⣬��ȥ��
��P��������0��3����
�ڵ�PM=MQʱ����P������ΪP��b��3�������У�
PQ=
��PM=
��
��
=
��
���b=-1��
��P��������-1��3����
������������P��������-1��3������0��3����
��3����0��t��4ʱ��S=-
t+
��Smax=
��
��4��t��5ʱ��S=-
t+
��Smax=
��
��5��t��8��S=
t-
��Smax=
��
���ı���MCDQ�����S�ķ�Χ��0��S��
��

��2������PMQ��������Գ�ͼ�Σ����PMQ��Ϊ���������Σ�
�ٵ�PQ=PMʱ����P������ΪP��a��3�������У�
PQ=
| (a-1)2+(3-2)2 |
| a2-2a+2 |
��֪MQ=
| 2 |
��
| a2-2a+2 |
| 2 |
���a=2��a=0��
��a=2ʱ��AP=4+2=6����t=6�������⣬��ȥ��
��P��������0��3����
�ڵ�PM=MQʱ����P������ΪP��b��3�������У�
PQ=
| b2-2b+2 |
| b2+4 |
��
| b2-2b+2 |
| b2+4 |
���b=-1��
��P��������-1��3����
������������P��������-1��3������0��3����
��3����0��t��4ʱ��S=-
| 7 |
| 4 |
| 21 |
| 2 |
| 21 |
| 2 |
��4��t��5ʱ��S=-
| 7 |
| 4 |
| 21 |
| 2 |
| 7 |
| 2 |
��5��t��8��S=
| 7 |
| 4 |
| 21 |
| 2 |
| 7 |
| 2 |
���ı���MCDQ�����S�ķ�Χ��0��S��
| 21 |
| 2 |
�����������ǵ���˶������⣬������ͼ������������������ε��ж���һ�δκ�����Ӧ�õ�֪ʶ���ۺ���ǿ���ѶȽϴ�

��ϰ��ϵ�д�
 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�
�����Ŀ
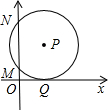 ��֪��ͼ����ƽ��ֱ������ϵ�У���P�ڵ�һ���ޣ���P��x�������ڵ�Q����y�ύ�ڵ�M��0��2����N��0��8������P�����꣮
��֪��ͼ����ƽ��ֱ������ϵ�У���P�ڵ�һ���ޣ���P��x�������ڵ�Q����y�ύ�ڵ�M��0��2����N��0��8������P�����꣮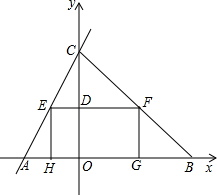 ��֪��ͼ����ƽ��ֱ������ϵ�У�A��-4��0����B��8��0����C��0��8����EΪ��ABC��AC����һ���㣨����A��C�غϣ�����EΪһ����������EFGH��ʹG��H����x���ϣ�F����BC�ϣ�EF��y����D�㣮����EH��Ϊx��
��֪��ͼ����ƽ��ֱ������ϵ�У�A��-4��0����B��8��0����C��0��8����EΪ��ABC��AC����һ���㣨����A��C�غϣ�����EΪһ����������EFGH��ʹG��H����x���ϣ�F����BC�ϣ�EF��y����D�㣮����EH��Ϊx�� ��֪��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�Ǿ��Σ���A��C������ֱ�ΪA��20��0����C��0��8������D��OA���е㣬��P��BC�����˶�������ODP������Ϊ10�ĵ���������ʱ����P������Ϊ
��֪��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�Ǿ��Σ���A��C������ֱ�ΪA��20��0����C��0��8������D��OA���е㣬��P��BC�����˶�������ODP������Ϊ10�ĵ���������ʱ����P������Ϊ