题目内容
(2013•苏州一模)如图①中,PB切半⊙O于B点,AB为直径,PA交⊙O于D点,连结BD,OD,已知图①中测得PD=2,AD=8.
(1)在图①中,求证:∠P=∠ODB;
(2)在图①中,求⊙O的半径;
(3)小军继续进行探究,在图①中保持⊙O的半径不变,且∠P的大小也不改变移动P点至图②位置,在移动过程中,小军发现DC的长度不改变,请求出DC的长度.

(1)在图①中,求证:∠P=∠ODB;
(2)在图①中,求⊙O的半径;
(3)小军继续进行探究,在图①中保持⊙O的半径不变,且∠P的大小也不改变移动P点至图②位置,在移动过程中,小军发现DC的长度不改变,请求出DC的长度.

分析:(1)根据切线的性质得∠PBA=90°,根据圆周角定理的推论得到∠ADB=90°,再利用等角的余角相等得∠P=∠ABD,由OD=OB得∠OBD=∠ODB,然后利用等量代换即可得到∠P=∠ODB;
(2)易证得△ABD∽△APB,利用AD:AB=AB:AP可计算出AB,则即可得到⊙O的半径;
(3)先在图①中计算出cosP=
,在图②中,作OH⊥DC于H,连结AC,根据垂径定理得DH=CH,由AB为直径得∠ACB=90°,由于∠P的大小不改变,则可判断∠PAC的大小也不改变,根据圆周角定理可判断DC的长度不改变,且∠DOC=2∠1,而∠DOC=2∠2,则∠1=∠2,根据等角的余角相等得∠P=∠ODH,所以cos∠ODH=cos∠P=
,然后在Rt△OHD中利用余弦定理可计算出DH,则即可得到DC的长.
(2)易证得△ABD∽△APB,利用AD:AB=AB:AP可计算出AB,则即可得到⊙O的半径;
(3)先在图①中计算出cosP=
| ||
| 5 |
| ||
| 5 |
解答:(1)证明:如图①,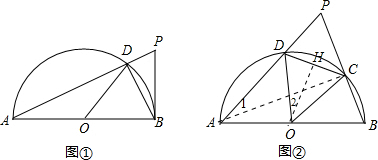
∵PB切半⊙O于B点,
∴PB⊥AB,
∴∠PBA=90°,
∴∠ABD+∠DBP=90°,
∵AB为直径,
∴∠ADB=90°,
∴∠P+∠DBP=90°,
∴∠P=∠ABD,
∵OD=OB,
∴∠OBD=∠ODB,
∴∠P=∠ODB;
(2)解:如图①,
∵∠ADB=∠ABP=90°,
而∠DAB=∠BAP,
∴△ABD∽△APB,
∴AD:AB=AB:AP,
∴AB2=AD•AP=AD•(AD+PD)=8×10,
∴AB=4
,
∴⊙O的半径为2
;
(3)解:在图①中,PB=
=2
cosP=
=
=
,
在图②中,作OH⊥DC于H,连结AC,则DH=CH,
∵AB为直径,
∴∠ACB=90°,
∵∠P的大小不改变,
∴∠PAC的大小也不改变,
∴DC的长度不改变,
∵∠DOC=2∠1,
而∠DOC=2∠2,
∴∠1=∠2,
∴∠P=∠ODH,
∴cos∠ODH=cos∠P=
,
而OD=2
,
∴cos∠ODH=
=
,
∴DH=2,
∴DC=2DH=4.

∵PB切半⊙O于B点,
∴PB⊥AB,
∴∠PBA=90°,
∴∠ABD+∠DBP=90°,
∵AB为直径,
∴∠ADB=90°,
∴∠P+∠DBP=90°,
∴∠P=∠ABD,
∵OD=OB,
∴∠OBD=∠ODB,
∴∠P=∠ODB;
(2)解:如图①,
∵∠ADB=∠ABP=90°,
而∠DAB=∠BAP,
∴△ABD∽△APB,
∴AD:AB=AB:AP,
∴AB2=AD•AP=AD•(AD+PD)=8×10,
∴AB=4
| 5 |
∴⊙O的半径为2
| 5 |
(3)解:在图①中,PB=
| PA2-AB2 |
| 5 |
cosP=
| PB |
| PA |
2
| ||
| 10 |
| ||
| 5 |
在图②中,作OH⊥DC于H,连结AC,则DH=CH,
∵AB为直径,
∴∠ACB=90°,
∵∠P的大小不改变,
∴∠PAC的大小也不改变,
∴DC的长度不改变,
∵∠DOC=2∠1,
而∠DOC=2∠2,
∴∠1=∠2,
∴∠P=∠ODH,
∴cos∠ODH=cos∠P=
| ||
| 5 |
而OD=2
| 5 |
∴cos∠ODH=
| DH |
| OD |
| ||
| 5 |
∴DH=2,
∴DC=2DH=4.
点评:本题考查了圆的综合题:熟练掌握垂径定理及其推论、圆周角定理及其推论和切线的性质,且运用它们进行几何证明;会利用相似比、勾股定理和锐角三角函数的定义进行几何计算.

练习册系列答案
相关题目
 (2013•苏州一模)如图,在平面直角坐标系中,点D为y轴上一点,⊙D与坐标轴分别相交于A(-
(2013•苏州一模)如图,在平面直角坐标系中,点D为y轴上一点,⊙D与坐标轴分别相交于A(- (2013•苏州一模)如图,正方形ABCD中,BE=CF.
(2013•苏州一模)如图,正方形ABCD中,BE=CF.