题目内容
 (2013•苏州一模)如图,在平面直角坐标系中,点D为y轴上一点,⊙D与坐标轴分别相交于A(-
(2013•苏州一模)如图,在平面直角坐标系中,点D为y轴上一点,⊙D与坐标轴分别相交于A(-| 3 |
(1)求⊙D的半径.
(2)E为优弧AB上一动点(不与A,B,C三点重合),M为半径DE的中点,连接M0,若∠MOD=α°,弧CE的长为y,求y与α之间的函数关系式;
(3)在(2)的条件下,过点E作EN⊥x轴于点N连接MN,当∠ENM=15°时,求E点的坐标,并判断以DE为直径的⊙M与直线DN的位置关系.
分析:(1)连接AD,设AD=r,则OD=OC-CD=OC-AD=3-r,在直角三角形ADO中利用勾股定理建立关于x的方程,解方程求出x的值即可;
(2)连接DE,EF,OM,由(1)可知圆的半径为2,所以DF=2,因为OD=OC-CD=3-2=1,所以OD=OF,因为M为半径DE的中点,所以OM是△DEF的中位线,OM∥EF,由平行线的性质和圆周角定理以及弧长公式即可求出弧CE的长即y与α之间的函数关系式;
(3)过D作DH⊥EN于H点,则HN=OD=1,延长NM交y轴于点P,连接OM,在Rt△DHE中,DE=2,DH=1,EH=
,ON=DH=1,EN=1+
,所以E(1,1+
),根据轴对称性可知,点E在第二象限的对称点(-1,
+1),故点E的坐标为:(1,
+1)或(-1,
+1).
(2)连接DE,EF,OM,由(1)可知圆的半径为2,所以DF=2,因为OD=OC-CD=3-2=1,所以OD=OF,因为M为半径DE的中点,所以OM是△DEF的中位线,OM∥EF,由平行线的性质和圆周角定理以及弧长公式即可求出弧CE的长即y与α之间的函数关系式;
(3)过D作DH⊥EN于H点,则HN=OD=1,延长NM交y轴于点P,连接OM,在Rt△DHE中,DE=2,DH=1,EH=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答:解:(1)连接AD(如图1),设AD=r,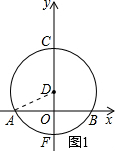
∵A(-
,0)、C(0,3)
∴AO=
,OC=3,
∴OD=OC-CD=OC-AD=3-r,
在Rt△AOD中,AD2=OD2+AO2,
∴r2=(3-r)2+
2,
解得:r=2,
∴⊙D的半径是2;
(2)连接DE,EF,OM(如图2),
由(1)可知圆的半径为2,∴DF=2,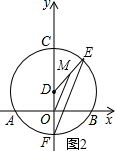
∵OD=OC-CD=3-2=1,
∴OD=OF,
∵M为半径DE的中点,
∴OM是△DEF的中位线,
∴OM∥EF,
∴∠MOD=∠DFE=
∠EDC,
∵∠MOD=α°,
∴弧CE的长为y=
=
=
;
(3)过D作DH⊥EN于H点,则HN=OD=1,延长NM交y轴于点P,连接OM(如图3),
易证△ENM≌△DPM,
∵MP=NM,∠PON=90°,OM=MP,
∴∠MOP=∠MPO,
∴∠OMN=2∠OPM,
∵OD=DM,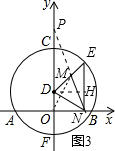
∴∠DOM=∠DMO,
∴∠DMN=∠POM+2∠OPM=3∠OPM,
∴∠DMN=3∠MNE,∠DMN=45°,
∵∠MNE=15°,
∴∠E=30°
在Rt△DHE中,DE=2,DH=1,EH=
,ON=DH=1,EN=1+
,
∴E(1,1+
),
根据轴对称性可知,点E在第二象限的对称点(-1,
+1),
故点E的坐标为:(1,
+1)或(-1,
+1).
以DE为直径的⊙M与直线DN的位置关系是:相交.

∵A(-
| 3 |
∴AO=
| 3 |
∴OD=OC-CD=OC-AD=3-r,
在Rt△AOD中,AD2=OD2+AO2,
∴r2=(3-r)2+
| 3 |
解得:r=2,
∴⊙D的半径是2;
(2)连接DE,EF,OM(如图2),
由(1)可知圆的半径为2,∴DF=2,
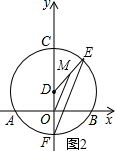
∵OD=OC-CD=3-2=1,
∴OD=OF,
∵M为半径DE的中点,
∴OM是△DEF的中位线,
∴OM∥EF,
∴∠MOD=∠DFE=
| 1 |
| 2 |
∵∠MOD=α°,
∴弧CE的长为y=
| nπr |
| 180 |
| 2απ×2 |
| 180 |
| πα |
| 45 |
(3)过D作DH⊥EN于H点,则HN=OD=1,延长NM交y轴于点P,连接OM(如图3),
易证△ENM≌△DPM,
∵MP=NM,∠PON=90°,OM=MP,
∴∠MOP=∠MPO,
∴∠OMN=2∠OPM,
∵OD=DM,

∴∠DOM=∠DMO,
∴∠DMN=∠POM+2∠OPM=3∠OPM,
∴∠DMN=3∠MNE,∠DMN=45°,
∵∠MNE=15°,
∴∠E=30°
在Rt△DHE中,DE=2,DH=1,EH=
| 3 |
| 3 |
∴E(1,1+
| 3 |
根据轴对称性可知,点E在第二象限的对称点(-1,
| 3 |
故点E的坐标为:(1,
| 3 |
| 3 |
以DE为直径的⊙M与直线DN的位置关系是:相交.
点评:本题考查了勾股定理的运用、全等三角形的判定和性质、三角形中位线定理、圆周角定理以及圆的轴对称的性质和弧长公式的运用,题目的综合性很强,对学生的解题能力要求很高.

练习册系列答案
相关题目
 (2013•苏州一模)如图,正方形ABCD中,BE=CF.
(2013•苏州一模)如图,正方形ABCD中,BE=CF.