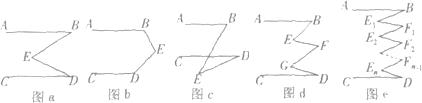
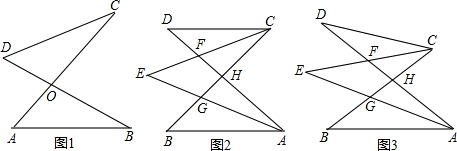
题目内容
28、如图①，若AB∥CD，点P在AB，CD外部，则有∠B=∠BOD，又∵∠BOD是△POD的外角，∴∠BOD=∠BPD+∠D，得∠BPD=∠B-∠D．
若将点P移到AB、CD内部，如图②，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何关系？请证明你的结论；
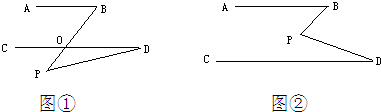
若将点P移到AB、CD内部，如图②，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何关系？请证明你的结论；
分析：延长BP交CD于点O，根据两直线平行，内错角相等可得∠B=∠POD，再利用三角形的一个外角等于与它不相邻的两个内角的和即可得解．
解答：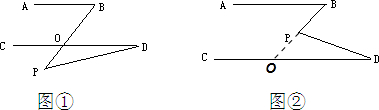
解：图②中，∠BPD=∠B+∠D．
理由如下：
延长BP交CD于点O，
∵AB∥CD，
∴∠B=∠POD，
在△POD中，∠BPD=∠POD+∠D，
∴∠BPD=∠B+∠D．
解：图②中，∠BPD=∠B+∠D．理由如下：
延长BP交CD于点O，
∵AB∥CD，
∴∠B=∠POD，
在△POD中，∠BPD=∠POD+∠D，
∴∠BPD=∠B+∠D．
点评：本题考查了两直线平行，内错角相等的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，读懂题目信息，理清求解思路是解题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
