Question

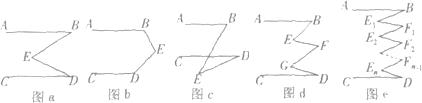
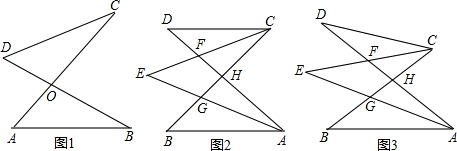
如图1，若AB∥CD，则有∠B+∠D=∠E．
（1）将点E移至图2的位置时，则∠B、∠D，∠E有什么关系？请证明你的结论．
（2）在图3中，∠E+∠G与∠B+∠F+∠D之间有什么关系？请证明你的结论．
（3）在图4中，若AB∥CD，又得到什么结论？（直接写出你的结论）．

Answer 1

分析：（1）过点E作EF∥AB，由AB∥CD，可得AB∥EF∥CD，根据两直线平行，同旁内角互补，即可求得∠B+∠BED+∠D=360°；
（2）过点E作EM∥AB，过点F作FN∥AB，过点G作GH∥AB，由AB∥CD，可得AB∥EM∥FN∥GH∥CD，然后根据两直线平行，内错角相等，即可求得∠E+∠G=∠B+∠F+∠D；
（3）由图1与图2可得规律：开口朝左的所有角度之和与开口朝右的所有角度之和相等，即可得∠E₁+∠E₂+…+∠E_n=∠B+∠F₁+∠F₂+…+∠F_n+∠D．

解答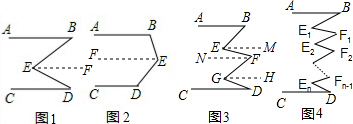：解：（1）∠B+∠D+∠E=360°．理由如下：
过点E作EF∥AB，
又∵AB∥CD，
∴AB∥EF∥CD，
∴∠B+∠BEF=180°，∠FED+∠D=180°，
∴∠B+∠BED+∠D=360°，
即∠B+∠D+∠E=360°；

（2）∠E+∠G=∠B+∠F+∠D．理由如下：
过点E作EM∥AB，过点F作FN∥AB，过点G作GH∥AB，
∵AB∥CD，
∴AB∥EM∥FN∥GH∥CD，
∴∠B=∠BEM，∠MEF=∠EFN，∠NFG=∠FGH，∠HGD=∠D，
∴∠BEF+∠FGD=∠BEM+∠MEF+∠FGH+∠HGD=∠B+∠EFN+∠NFG+∠D=∠B+∠EFG+∠D，
即∠E+∠G=∠B+∠F+∠D．

（3）∠E₁+∠E₂+…+∠E_n=∠B+∠F₁+∠F₂+…+∠F_n+∠D．理由如下：
由图1与图3可得：开口朝左的所有角度之和与开口朝右的所有角度之和相等，
∴∠E₁+∠E₂+…+∠E_n=∠B+∠F₁+∠F₂+…+∠F_n+∠D．

点评：此题考查了平行线的性质．此题难度较大，属于规律性题目，注意掌握辅助线的作法，注意发现规律：开口朝左的所有角度之和与开口朝右的所有角度之和相等是解此题的关键．