题目内容
【题目】如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过秒时,△DEB与△BCA全等. 
【答案】4,12,16
【解析】解:设点E经过t秒时,△DEB≌△BCA;此时AE=3t
分情况讨论:(1)当点E在点B的左侧时,
BE=24﹣3t=12,
∴t=4;(2)当点E在点B的右侧时,
①BE=AC时,3t=24+12,
∴t=12;
②BE=AB时,
3t=24+24,
∴t=16.
综上所述,故答案为:4,12,16.
设点E经过t秒时,△DEB≌△BCA;由斜边ED=CB,分类讨论BE=AC或BE=AB时的情况,求出t的值即可.

练习册系列答案
相关题目
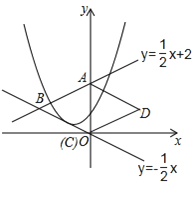
【题目】直线![]() 与
与![]() 轴交于点A,与直线
轴交于点A,与直线![]() 交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线
交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,若抛物线与菱形的边AB、BC都有公共点,则
上移动,若抛物线与菱形的边AB、BC都有公共点,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计。并绘制了统计表.
零花钱数额(元) | 5 | 1 | 15 | 20 |
学生人数(人) | a | 15 | 20 | 5 |
请根据图表中的信息回答以下问题.
(1)求a的值;
(2)求这50名学生每人一周内的零花钱数额的众数和平均数。