题目内容
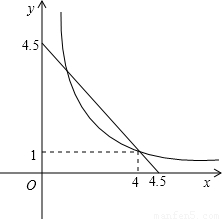
 如图,在同一平面直角坐标系中作出相应的两个一次函数的图象,则不等式组
如图,在同一平面直角坐标系中作出相应的两个一次函数的图象,则不等式组
|
分析:求不等式组
的解集,就是求直线l1的x轴上方,以及直线l2在x轴下边的部分,自变量x的取值范围.
|
解答:解:直线l1的x轴上方,以及直线l2在x轴下边的部分,自变量x的取值范围是:x>3.
故不等式组
的解集是:x>3
故填:x>3.
故不等式组
|
故填:x>3.
点评:能够由不等式的问题转化为求函数自变量取值范围的问题是解决本题的关键.

练习册系列答案
相关题目
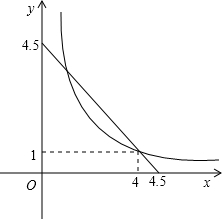 由题意得方程组:
由题意得方程组: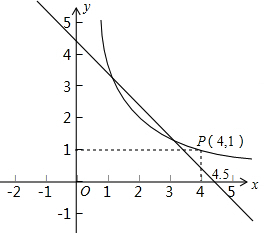 (2012•西城区模拟)探索一个问题:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”
(2012•西城区模拟)探索一个问题:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”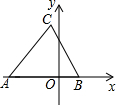 如图,在同一平面直角坐标系中,△ABC的顶点坐标分别为A(-6,0),B(2,0),C(-1,8),则△ABC的面积是
如图,在同一平面直角坐标系中,△ABC的顶点坐标分别为A(-6,0),B(2,0),C(-1,8),则△ABC的面积是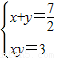 ,消去y化简得:2x2-7x+6=0,
,消去y化简得:2x2-7x+6=0,