题目内容
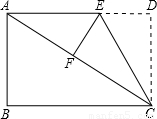
(2006•邵阳)如图,在矩形ABCD中,AB=6,BC=8.将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.(1)求EF的长;
(2)求梯形ABCE的面积.
【答案】分析:(1)根据折叠的性质,折叠前后边相等,即CF=CD,DE=EF,得:AE=AD-EF,在Rt△ACD中,根据勾股定理,可将AC的长求出,知CF的长,可求出AF的长,在Rt△AEF中,根据AE2=EF2+AF2,可将EF的长求出;
(2)根据S梯形=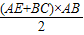 ,将各边的长代入进行求解即可.
,将各边的长代入进行求解即可.
解答:解:(1)设EF=x依题意知:△CDE≌△CFE,
∴DE=EF=x,CF=CD=6.
∵在Rt△ACD中,AC=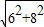 =10,
=10,
∴AF=AC-CF=4,AE=AD-DE=8-x.
在Rt△AEF中,有AE2=AF2+EF2
即(8-x)2=42+x2
解得x=3,即:EF=3.
(2)由(1)知:AE=8-3=5,
∴S梯形ABCE=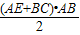 =(5+8)×6÷2=39.
=(5+8)×6÷2=39.
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后边相等.
(2)根据S梯形=
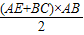 ,将各边的长代入进行求解即可.
,将各边的长代入进行求解即可.解答:解:(1)设EF=x依题意知:△CDE≌△CFE,
∴DE=EF=x,CF=CD=6.
∵在Rt△ACD中,AC=
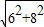 =10,
=10,∴AF=AC-CF=4,AE=AD-DE=8-x.
在Rt△AEF中,有AE2=AF2+EF2
即(8-x)2=42+x2
解得x=3,即:EF=3.
(2)由(1)知:AE=8-3=5,
∴S梯形ABCE=
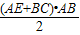 =(5+8)×6÷2=39.
=(5+8)×6÷2=39.点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后边相等.

练习册系列答案
相关题目
 (2006•邵阳)如图,若将△ABC绕点O顺时针旋转180°后得到△A′B′C′,则A点的对应点A′点的坐标是
(2006•邵阳)如图,若将△ABC绕点O顺时针旋转180°后得到△A′B′C′,则A点的对应点A′点的坐标是 x2+1,直线y=kx+b经过点B(0,2)
x2+1,直线y=kx+b经过点B(0,2) x2+1相交,其中一个交点为P,求出P的坐标;
x2+1相交,其中一个交点为P,求出P的坐标;
 x2+1,直线y=kx+b经过点B(0,2)
x2+1,直线y=kx+b经过点B(0,2) x2+1相交,其中一个交点为P,求出P的坐标;
x2+1相交,其中一个交点为P,求出P的坐标;
