题目内容
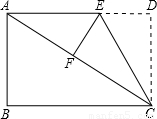
(2006•邵阳)如图,已知抛物线y= x2+1,直线y=kx+b经过点B(0,2)
x2+1,直线y=kx+b经过点B(0,2)(1)求b的值;
(2)将直线y=kx+b绕着点B旋转到与x轴平行的位置时(如图1),直线与抛物线y=
 x2+1相交,其中一个交点为P,求出P的坐标;
x2+1相交,其中一个交点为P,求出P的坐标;(3)将直线y=kx+b继续绕着点B旋转,与抛物线相交,其中一个交点为P'(如图②),过点P'作x轴的垂线P'M,点M为垂足.是否存在这样的点P',使△P'BM为等边三角形?若存在,请求出点P'的坐标;若不存在,请说明理由.

【答案】分析:(1)将B点的坐标代入直线的解析式中即可得出b的值.
(2)直线绕B旋转到与x轴平行的位置,此时直线的解析式为y=2,然后联立抛物线的解析式即可求出交点P的坐标.
(3)如果△P′BM是等边三角形,那么∠BP′M=60°,不难得出BP′的长正好等于P′,B两点纵坐标差的绝对值的2倍.据此可求出P′的纵坐标,进而可根据抛物线的解析式求出P′的坐标.
解答:解:(1)∵直线y=kx+b过点B(0,2),
∴b=2.
(2)y=kx+b绕点B旋转到与x轴平行,即y=2,
∴P(2,2)或P(-2,2),
依题意有: x2+1=2,
x2+1=2,
x=±2,
∴P(2,2)或P(-2,2).
(3)假设存在点P'(x,y),使△P'BM为等边三角形,
如图,则∠BP'M=60°
P'M=yP'B=2(P'M-2)=2(y-2)
且P'M=P'B
即y=2(y-2)
y=4
又点P′在抛物线y= x2+1上
x2+1上
∴ x2+1=4
x2+1=4
x=±2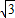
∴当直线y=kx+b绕点B旋转时与抛物线y= x2+1相交,存在一个交点P′(2
x2+1相交,存在一个交点P′(2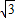 ,4)或P′(-2
,4)或P′(-2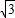 ,4)
,4)
使△P'BM为等边三角形.
点评:本题主要考查一次函数解析式的确定、函数图象的旋转和平移、函数图象交点、等边三角形的判定和性质等知识以及综合应用知识、解决问题的能力.
(2)直线绕B旋转到与x轴平行的位置,此时直线的解析式为y=2,然后联立抛物线的解析式即可求出交点P的坐标.
(3)如果△P′BM是等边三角形,那么∠BP′M=60°,不难得出BP′的长正好等于P′,B两点纵坐标差的绝对值的2倍.据此可求出P′的纵坐标,进而可根据抛物线的解析式求出P′的坐标.
解答:解:(1)∵直线y=kx+b过点B(0,2),
∴b=2.
(2)y=kx+b绕点B旋转到与x轴平行,即y=2,
∴P(2,2)或P(-2,2),
依题意有:
 x2+1=2,
x2+1=2,x=±2,
∴P(2,2)或P(-2,2).
(3)假设存在点P'(x,y),使△P'BM为等边三角形,
如图,则∠BP'M=60°
P'M=yP'B=2(P'M-2)=2(y-2)
且P'M=P'B
即y=2(y-2)
y=4
又点P′在抛物线y=
 x2+1上
x2+1上∴
 x2+1=4
x2+1=4x=±2
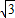
∴当直线y=kx+b绕点B旋转时与抛物线y=
 x2+1相交,存在一个交点P′(2
x2+1相交,存在一个交点P′(2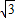 ,4)或P′(-2
,4)或P′(-2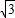 ,4)
,4)使△P'BM为等边三角形.
点评:本题主要考查一次函数解析式的确定、函数图象的旋转和平移、函数图象交点、等边三角形的判定和性质等知识以及综合应用知识、解决问题的能力.

练习册系列答案
相关题目
 (2006•邵阳)如图,若将△ABC绕点O顺时针旋转180°后得到△A′B′C′,则A点的对应点A′点的坐标是
(2006•邵阳)如图,若将△ABC绕点O顺时针旋转180°后得到△A′B′C′,则A点的对应点A′点的坐标是 x2+1,直线y=kx+b经过点B(0,2)
x2+1,直线y=kx+b经过点B(0,2) x2+1相交,其中一个交点为P,求出P的坐标;
x2+1相交,其中一个交点为P,求出P的坐标;