题目内容
【题目】已知四边形ABCD中,AD∥BC,∠D=90°,AC平分∠BAD,∠ACD=30°
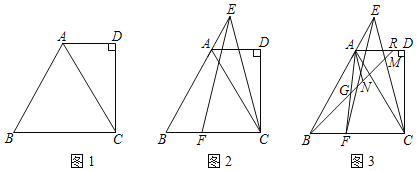
(1)如图1,求证:△ABC是等边三角形;
(2)如图2,点E在边BA的延长线上,在边BC上取一点F,连接EC、EF且EC=EF,求证:BF=AE;
(3)如图3,在(2)的条件下,连接AF,取AF的中点G,连接BG并延长交线段EC于M,交线段AD于R,过点A做AN∥EC交线段BR于N,若GN=2,EM=5,求CM的长.
【答案】(1)见解析;(2)见解析;(3)CM=9.
【解析】
(1)根据三个角是60°的三角形是等边三角形即可证明.
(2)如图2中,作FM∥AC交AB于M.证明△BMF是等边三角形,△EMF≌△CAE(AAS)即可解决问题.
(3)如图3中,连接AM,ER.证明△AGR≌△FGB(AAS),△EBR≌△BEF(SAS),再证明△AMN是等边三角形,证明∠ANR≌△AME(SAS),推出EM=RN=5,证明BR=EF=EC=7即可解决问题.
(1)证明:∵∠D=90°,∠ACD=30°,
∴∠CAD=60°,
∵AC平分∠BAD,
∴∠CAB=∠CAD=60°,
∵AD∥BC,
∴∠DAC=∠BCA=60°,
∴∠B=∠BCA=∠BAC=60°,
∴△ABC是等边三角形.
(2)证明:如图2中,作FM∥AC交AB于M.
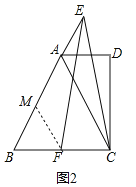
∵MF∥AC,
∴∠BMF=∠BAC=60°,∠BFM=∠BCA=60°,
∴∠B=∠BMF=∠BFM=60°,
∴△BMF是等边三角形,
∴MF=BF,∠EMF=120°=∠CAE,
∵EF=EC,
∴∠EFC=∠ECF,
∴∠MFE=180°﹣60°﹣∠EFC=120°﹣∠EFC,
∠AEC=180°﹣60°﹣∠ECB=120°﹣∠ECF,
∴∠MFE=∠AEC,在△EMF和△CAE中,
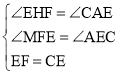 ,
,
∴△EMF≌△CAE(AAS),
∴MF=AE,
∴BF=AE.
(3)解:如图3中,连接AM,ER.
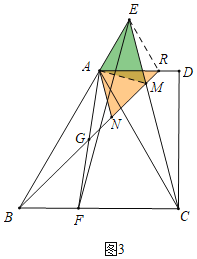
∵AR∥BF,
∴∠ARG=∠GFB,∠EAR=∠ABC=60°,
∵∠AGR=∠FGB,AG=GF,
∴△AGR≌△FGB(AAS),
∴AR=BF,RG=BG,
∵AE=BF,
∴AE=AR,
∴△AER是等边三角形,
∴ER=AE=BF,∠BER=∠EBF=60°,
∵BE=EB,
∴△EBR≌△BEF(SAS),
∴∠BEF=∠EBR,EF=BR,
∵∠BEF=∠ACE,
∴∠ABM=∠ACM,
∴A,B,C,M四点共圆,
∴∠CMB=∠CAB=60°,
∴∠EMR=∠EAR=60°,
∴A,E,R,M四点共圆,
∴∠AMF=∠ARE=60°,
∵AN∥EC,
∴∠ANM=∠NMC=60°,∠NAM=∠AME=60°,
∴△AMN是等边三角形,
∴AN=AM,
∵∠NAM=∠EAR=60°,
∴∠NAR=∠MAE,
∵AR=AE,
∴∠ANR≌△AME(SAS),
∴EM=RN=5,
∵GN=2,
∴GR=GB=2+5=7,
∴BR=EF=EC=14,
∴CM=EC﹣EM=14﹣5=9.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某中学八⑴班、⑵班各选5名同学参加“爱我中华”演讲比赛,其预赛成绩(满分100分)如图所示:
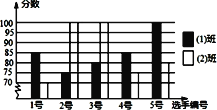
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | |
八(1)班 | 85 | 85 | |
八(2)班 | 85 | 80 |
(2)根据两班成绩的平均数和中位数,分析哪班成绩较好?
(3)如果每班各选2名同学参加决赛,你认为哪个班实力更强些?请说明理由.