题目内容
【题目】如图,⊙O直径AB和弦CD相交于点E,AE=4,EB=8,∠DEB=30°,求弦CD长.

【答案】![]()
【解析】试题分析:过O作OF垂直于CD,连接OD,利用垂径定理得到F为CD的中点,由AE+EB求出直径AB的长,进而确定出半径OA与OD的长,由OA-AE求出OE的长,在直角三角形OEF中,利用30°所对的直角边等于斜边的一半求出OF的长,在直角三角形ODF中,利用勾股定理求出DF的长,由CD=2DF即可求出CD的长.
试题解析:过O作OF⊥CD,交CD于点F,连接OD,
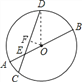
∴F为CD的中点,即CF=DF,
∵AE=4,EB=8,
∴AB=AE+EB=4+8=12,
∴OA=6,
∴OE=OAAE=64=2,
在Rt△OEF中,∠DEB=30°,
∴OF=![]() OE=1,
OE=1,
在Rt△ODF中,OF=1,OD=6,
根据勾股定理得:DF=![]() =
=![]() ,
,
则CD=2DF=2![]() .
.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目