题目内容
有下列命题:①若3x+2y=0,则x=y=0;②若x(1-x)=0,则x=0;③一元二次方程ax2+bx+c=0,若ac<0,则方程必定有实数解;④若| (x-1)2 |
分析:本题需先根据真命题和假命题的定义判断出各题的真假,最后得出结果即可.
解答:解:①若3x+2y=0,可以解得2y=-3x,可以求得很多结果,故x=y=0,是假命题;
若x(1-x)=0,可以解得x=0,或x=1,故②是假命题;
在一元二次方程中,判别式b2-4ac>0,则方程有两个不相等的实数根,因为ac<0,则判别式b2-4ac一定大于0,是真命题;
若
=x-1,则x≥1,故④是假命题.
故题目中有一个真命题.
故答案为③.
若x(1-x)=0,可以解得x=0,或x=1,故②是假命题;
在一元二次方程中,判别式b2-4ac>0,则方程有两个不相等的实数根,因为ac<0,则判别式b2-4ac一定大于0,是真命题;
若
| (x-1)2 |
故题目中有一个真命题.
故答案为③.
点评:主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
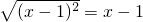 ,则x>1,其中是真命题的是________.
,则x>1,其中是真命题的是________.