ЬтФПФкШн
ЁОЬтФПЁПШчЭМЂйЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуAЃЈЃ5ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉЃЌDЃЈ2ЃЌ7ЃЉЃЎ
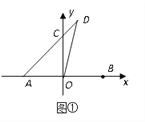
ЃЈ1ЃЉШєЕуCЮЊADгыyжсЕФНЛЕуЃЌЧѓCЕуЕФзјБъЃЛЁОЬсЪОЃКЩшCЕуЕФзјБъЮЊЃЈ0ЃЌxЃЉЁП
ЃЈ2ЃЉЖЏЕуPДгBЕуГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШбиBAЗНЯђдЫЖЏЃЌЭЌЪБЖЏЕуQДгCЕуГіЗЂЃЌвВвдУПУы1ИіЕЅЮЛЕФЫйЖШбиyжсе§АыжсЗНЯђдЫЖЏЃЎЃЈЕБPЕудЫЖЏЕНAЕуЪБЃЌСНЕуЖМЭЃжЙдЫЖЏЃЌШчЭМЂкЫљЪОЃЉЃЎЩшДгГіЗЂЦ№дЫЖЏСЫxУыЃЎ
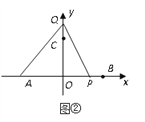
ЂйЧыгУКЌxЕФДњЪ§ЪНЗжБ№БэЪОPЁЂQСНЕуЕФзјБъЃЛ
ЂкЕБxЃН2ЪБЃЌyжсЩЯЪЧЗёДцдквЛЕуEЃЌЪЙЕУЁїAQEЕФУцЛ§гыЁїAPQЕФУцЛ§ЯрЕШЃПШєДцдкЃЌЧѓEЕуЕФзјБъЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ0ЃЌ5ЃЉЃЛЃЈ2ЃЉЂйЕуPЃЈ5ЃxЃЌ0ЃЉЃЌQЃЈ0ЃЌxЃЋ5ЃЉЃЛЂкДцдкЃЌ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЩшCЕузјБъЮЊЃЈ0, xЃЉ,гЩ![]() ЃЌНтД№МДПЩЃЛЃЈ2ЃЉЂйИљОнЬтвтЁЂНсКЯЭМаЮНтД№ЃЛ
ЃЌНтД№МДПЩЃЛЃЈ2ЃЉЂйИљОнЬтвтЁЂНсКЯЭМаЮНтД№ЃЛ
ЂкЗжEдкyжсЕФе§АыжсКЭEдкyжсЕФИКАыжсСНжжЧщПіЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМЦЫуМДПЩЃЎ
БОЬтНтЮіЃКЃЈ1ЃЉЩшCЕуЕФзјБъЮЊЃЈ0ЃЌxЃЉЃЌвРЬтвтЃЌга
![]() ЃЌ
ЃЌ
МДxЃН5ЃЌЙЪЕуCЕФзјБъЮЊЃЈ0ЃЌ5ЃЉЃЎ
ЃЈ2ЃЉЂйЕуPЃЈ5ЃxЃЌ0ЃЉЃЌQЃЈ0ЃЌxЃЋ5ЃЉ
ЂкЕБxЃН2ЪБЃЌPЃЈ3ЃЌ0ЃЉЃЌQЃЈ0ЃЌ7ЃЉ
ЩшEЃЈ0ЃЌyЃЉЃЌдђ![]() ЃЌ
ЃЌ![]() .Щш
.Щш![]() ЃЌЁр
ЃЌЁр![]() Лђ
Лђ![]() ЃЌЁр
ЃЌЁр![]() Лђ
Лђ![]() .
.
ЙЪДцдкетбљЕФЕуEЃЌЦфEЕФзјБъЮЊ![]() Лђ
Лђ![]() .
.

 дѕбљбЇКУХЃНђгЂгяЯЕСаД№АИ
дѕбљбЇКУХЃНђгЂгяЯЕСаД№АИ
