题目内容
已知:如图,在直角三角形ABC中,∠BAC=90°,AB=AC,D为BC的中点,E为AC上一点,点G在BE 上,连接DG并延长交AE于F,若∠FGE=45°.
上,连接DG并延长交AE于F,若∠FGE=45°.(1)求证:BD•BC=BG•BE;
(2)求证:AG⊥BE;
(3)若E为AC的中点,求EF:FD的值.
分析:(1)根据题意,易证△GBD∽△CBE,得
=
,即BD•BC=BG•BE;
(2)可通过证明ABG∽△EBA从而求得AG⊥BE;
(3)首先连接DE,E是AC中点,D是BC中点,得出DE∥BA,因为BA⊥AC,所以 DE⊥AC设AB=2a AE=a,做CH⊥BE交BE的延长线于H,再利用△AEG≌△CEH,以及△DEF∽△BHC得出即可.
| BD |
| BE |
| BG |
| BC |
(2)可通过证明ABG∽△EBA从而求得AG⊥BE;
(3)首先连接DE,E是AC中点,D是BC中点,得出DE∥BA,因为BA⊥AC,所以 DE⊥AC设AB=2a AE=a,做CH⊥BE交BE的延长线于H,再利用△AEG≌△CEH,以及△DEF∽△BHC得出即可.
解答:(1)证明:∵∠BAC=90°,AB=AC
∴∠ABC=∠C=45°
∵∠BGD=∠FGE=45°
∴∠C=∠BGD
∵∠GBC=∠GBC
∴△GBD∽△CBE
∴
=
即BD•BC=BG•BE;
(2)证明:∵BD•BC=BG•BE,∠C=45°,
∴BG=
=
=
=
,
∴
=
,∠ABG=∠EBA
∴△ABG∽△EBA
∴∠BGA=∠BAE=90°
∴AG⊥BE;
(3)解:连接DE,
连接DE,E是AC中点,D是BC中点,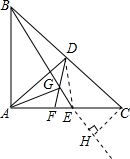
∴DE∥BA,
∵BA⊥AC,
∴DE⊥AC,设AB=2a AE=a,做CH⊥BE交BE的延长线于H,
∵∠AEG=∠CEH,∠AGE=∠CHE,AE=EC
∴△AEG≌△CEH(AAS),
∴CH=AG,
∠GAE=∠HCE
∵∠BAE为直角,
∴BE=
a,
∴AG=AB×
=
a=
a,
∴CH=
a,
∵AG⊥BE,∠FGE=45°,
∴∠AGF=45°=∠ECB,
∵∠FGE=45°,
∴∠AGE=90°,
∴AG∥CH,
∴∠GAE=∠HCE,
∵∠DFE=∠GAE+∠AGF=∠HCE+∠ECB;
∴∠DFE=∠BCH,
又∵DE⊥AC,CH⊥BE,
∴△DEF∽△BHC
∴EF:DF=CH:BC=
a:2
a=
.
∴∠ABC=∠C=45°
∵∠BGD=∠FGE=45°
∴∠C=∠BGD
∵∠GBC=∠GBC
∴△GBD∽△CBE
∴
| BD |
| BE |
| BG |
| BC |
即BD•BC=BG•BE;
(2)证明:∵BD•BC=BG•BE,∠C=45°,
∴BG=
| BD•BC |
| BE |
| ||
| BE |
| ||||
| BE |
| AB2 |
| BE |
∴
| AB |
| BG |
| BE |
| AB |
∴△ABG∽△EBA
∴∠BGA=∠BAE=90°
∴AG⊥BE;
(3)解:连接DE,
连接DE,E是AC中点,D是BC中点,

∴DE∥BA,
∵BA⊥AC,
∴DE⊥AC,设AB=2a AE=a,做CH⊥BE交BE的延长线于H,
∵∠AEG=∠CEH,∠AGE=∠CHE,AE=EC
∴△AEG≌△CEH(AAS),
∴CH=AG,
∠GAE=∠HCE
∵∠BAE为直角,
∴BE=
| 5 |
∴AG=AB×
| AE |
| BE |
| 2 | ||
|
2
| ||
| 5 |
∴CH=
2
| ||
| 5 |
∵AG⊥BE,∠FGE=45°,
∴∠AGF=45°=∠ECB,
∵∠FGE=45°,
∴∠AGE=90°,
∴AG∥CH,
∴∠GAE=∠HCE,
∵∠DFE=∠GAE+∠AGF=∠HCE+∠ECB;
∴∠DFE=∠BCH,
又∵DE⊥AC,CH⊥BE,
∴△DEF∽△BHC
∴EF:DF=CH:BC=
2
| ||
| 5 |
| 2 |
| ||
| 10 |
点评:考查相似三角形的判定和性质,通常情况乘积可以转化成比例的形式.

练习册系列答案
相关题目

 标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由.
标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由. 移动的时间是秒t,设△OPD的面积是S.
移动的时间是秒t,设△OPD的面积是S. 与等边三角形重叠部分的面积等于直角梯形ABCD的面积的一半,这时等边三角形的边长应为多少?
与等边三角形重叠部分的面积等于直角梯形ABCD的面积的一半,这时等边三角形的边长应为多少? 已知,如图,在直角坐标系中,S△ABC=24,∠ABC=45°,BC=12,求△ABC的三个顶点的坐标.
已知,如图,在直角坐标系中,S△ABC=24,∠ABC=45°,BC=12,求△ABC的三个顶点的坐标.