题目内容
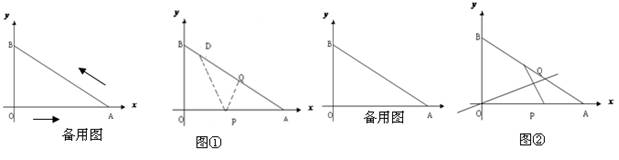
已知:如图,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系,A,B,C三点的坐标分别是A(8,0),B(8,10),C(0,4),点D(4,7)是CB的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OAB的路线移动, 移动的时间是秒t,设△OPD的面积是S.
移动的时间是秒t,设△OPD的面积是S.(1)求直线BC的解析式;
(2)请求出S与t的函数关系式,并指出自变量t的取值范围;
(3)求S的最大值;
(4)当9≤t<12时,求S的范围.
分析:(1)先设出BC的解析式,再分别将B、C的坐标代入解析式,进而得出所求;
(2)用t表示出P点坐标,进而表示P到OD的距离,再根据D点坐标求出OD长,然后表示出△OPD的面积;
(3)根据(2)中已经表示出的S与t的函数关系式,根据函数图象的随自变量的变化而变化的关系求出最大值;
(4)根据(2)中已经表示出的S与t的函数关系式和自变量的取值范围得出所求.
(2)用t表示出P点坐标,进而表示P到OD的距离,再根据D点坐标求出OD长,然后表示出△OPD的面积;
(3)根据(2)中已经表示出的S与t的函数关系式,根据函数图象的随自变量的变化而变化的关系求出最大值;
(4)根据(2)中已经表示出的S与t的函数关系式和自变量的取值范围得出所求.
解答: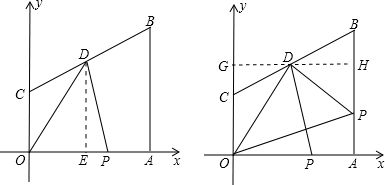 解:(1)直线BC过点C(0,4),
解:(1)直线BC过点C(0,4),
设直线BC解析式为y=kx+4,
将B(8,10)代入得y=
x+4;
(2)当0<t≤8时(2分)
过D作DE⊥OA于E点,则OP=t,DE=7
S=
OP×DE=
(3分)
当8<t≤18时(4分)
过D作GH⊥BA于H点,交y轴于点G,则DG=4,DH=4
AP=t-8,(5分)
BP=18-t(6分)
S=S梯形OABC-S△OCD-S△OAP-S△DPB
=
×8-
×4×4-
×8(t-8)-
(18-t)×4(7分)
=-2t+44;(8分)
(3)当0<t≤8时
当t=8时S的最大值是S=
=
=28(9分)
当8<t≤18时
S随着t的增大而减少,所以S无最大值(10分)
所以当t=8时S的最大值是28.(11分)
(4)9≤t<12时
-24<-2t≤-18
20<-2t+44≤26
即20<S≤26.(12分)
 解:(1)直线BC过点C(0,4),
解:(1)直线BC过点C(0,4),设直线BC解析式为y=kx+4,
将B(8,10)代入得y=
| 3 |
| 4 |
(2)当0<t≤8时(2分)
过D作DE⊥OA于E点,则OP=t,DE=7
S=
| 1 |
| 2 |
| 7t |
| 2 |
当8<t≤18时(4分)
过D作GH⊥BA于H点,交y轴于点G,则DG=4,DH=4
AP=t-8,(5分)
BP=18-t(6分)
S=S梯形OABC-S△OCD-S△OAP-S△DPB
=
| 4+10 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-2t+44;(8分)
(3)当0<t≤8时
当t=8时S的最大值是S=
| 7t |
| 2 |
| 7×8 |
| 2 |
当8<t≤18时
S随着t的增大而减少,所以S无最大值(10分)
所以当t=8时S的最大值是28.(11分)
(4)9≤t<12时
-24<-2t≤-18
20<-2t+44≤26
即20<S≤26.(12分)
点评:本题考查了二次函数的应用,是典型的数形结合的题目.

练习册系列答案
相关题目