题目内容
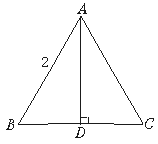
等边△ABC，AD为它的高线，如图所示，若它的边长为2，则它的周长为 ，AD= ，BD：AD：AB= ： ： ．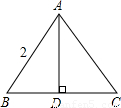
【答案】分析：根据等边三角形三线合一的性质可求得D为BC的中点，已知AB、BD的长，根据勾股定理即可求得AD的长，即可求BD：AD：AB．
解答：解：三角形三边长相等，∴三角形周长为边长的3倍等于6，
∵等边三角形三线合一，∴D为BC的中点，
即BD=DC=1，∴AD=
=
，
故答案为 6、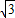
、1：
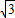：2．
点评：本题考查了勾股定理在直角三角形中的运用，考查了等边三角形三边相等的性质，本题中根据勾股定理计算AD的值是解题的关键．
解答：解：三角形三边长相等，∴三角形周长为边长的3倍等于6，
∵等边三角形三线合一，∴D为BC的中点，
即BD=DC=1，∴AD=
=，故答案为 6、
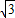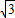、1：：2．点评：本题考查了勾股定理在直角三角形中的运用，考查了等边三角形三边相等的性质，本题中根据勾股定理计算AD的值是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
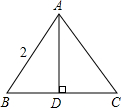等边△ABC，AD为它的高线，如图所示，若它的边长为2，则它的周长为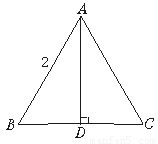
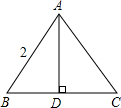等边△ABC，AD为它的高线，如图所示，若它的边长为2，则它的周长为________，AD=________，BD：AD：AB=________：________：________．