��Ŀ����
����Ŀ��С����һ���dz������е����꼶ѧ��������4����ȫһ�������ǰ壨��ͼ1��ƴ����һ���dz�������ͼ�Σ���ͼ2���������ʦ�Ժ��֪����ͼ����һ�������Σ�����������ı���Ҳ��һ�������Σ�Ϊ������һ����̽����С�������ǰ�����߳���Ϊa��b��c��ʾ����ͼ3���������������ηֱ���������ABCD��������EFGH��ʾ��Ȼ���������ֲ�ͬ�ķ���������������ABCD������� 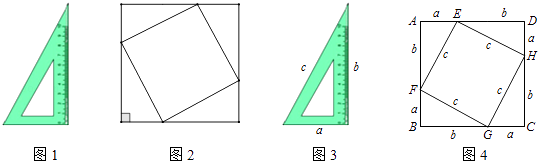
��1�����������ֲ�ͬ�ķ��������������ABCD����� ����һ����������
��2�����ݣ�1���м����������ܵõ���ô���Ľ��ۣ�
��3��������������������2���еõ��Ľ��ۣ�
���𰸡�
��1���⣺����һ��������ABCD�����=��a+b��2=a2+2ab+b2��
��������������ABCD�����=4 ![]() ab+c2=c2+2ab
ab+c2=c2+2ab
��2���⣺�ɣ�1����c2=a2+b2
��3���⣺���ۣ�ֱ�������ε���ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ��
����������1������һ��ֱ�����������ε������ʽ���㣻������������4��ֱ�������ε�����ͱ߳�Ϊc�������ε�����Ϳɵõ�������ABCD���������2��������������c2=a2+b2����3������Ϊ���ɶ�����