Question

23、如图，AC⊥BC，BD⊥AD，AC﹦BD，求证：BC﹦AD．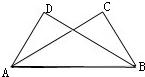
证明：∵AC⊥BC，BD⊥AD，
∴∠C=∠D=

90

°．
在Rt△ABC和Rt△BAD中，
AB=BA（

公共边

），AC=BD（已知）
∴Rt△ABC≌Rt△BAD（

HL

）．
∴BC﹦AD．

Answer 1

分析：由已知先证∠C=∠D=90°，即△ABC和△BAD是直角三角形，再已知AC=BD，AB又是公共边，故可根据HL判定Rt△ABC≌Rt△BAD，即证BC﹦AD．

解答：证明：∵AC⊥BC，BD⊥A
∴∠C=∠D=90°．
在Rt△ABC和Rt△BAD中，
AB=BA（公共边），AC=BD（已知）
∴Rt△ABC≌Rt△BAD（HL）．
∴BC﹦AD．

点评：本题考查填写证明过程中的理由，有助于更清晰的了解证明题的一般步骤．