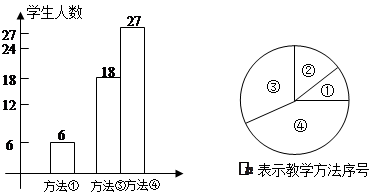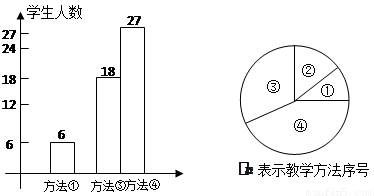题目内容
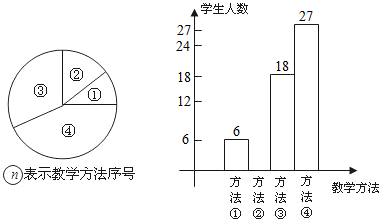
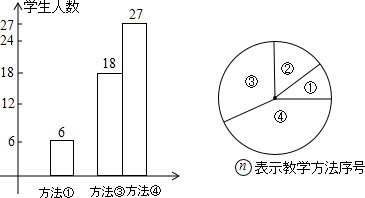
数学课上,年轻的刘老师在讲授“轴对称”时,设计了四种教学方法:①教师让学生对折纸,观察发现规律,然后画图.②教师让学生自己做.③教师引导学生画图,发现规律.④教师讲,学生听.刘老师将四种方法作为调查内容发到全年级8个班420名同学手中,要求每位同学选出自己最喜欢的一种,然后他从420份问卷中随机抽取了一部分同学的问卷答案,统计结果如图所示:
(1)求抽取问卷答案的学生人数;
(2)求抽取的问卷中喜欢第②种方法的人数,并补上条形图的空缺部分;
(3)全年级同学最喜欢的教学方法是哪一种?选择这种方法的大约有多少人?并计算扇形统计图中这种方法的人数所占扇形圆心角的大小.
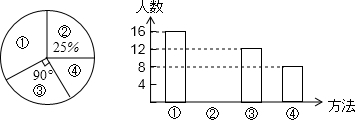
(1)求抽取问卷答案的学生人数;
(2)求抽取的问卷中喜欢第②种方法的人数,并补上条形图的空缺部分;
(3)全年级同学最喜欢的教学方法是哪一种?选择这种方法的大约有多少人?并计算扇形统计图中这种方法的人数所占扇形圆心角的大小.

分析:(1)根据喜欢③的人数及所占的比例即可得出抽取问卷答案的学生人数;
(2)根据(1)的答案,结合②所占的比例即可得出喜欢②种方法的人数,然后补全统计图即可;
(3)易得喜欢①的人数最多,先求出喜欢①的人数所占的比例,然后根据①所占的比例,可得出选择这种方法的大约人数.
(2)根据(1)的答案,结合②所占的比例即可得出喜欢②种方法的人数,然后补全统计图即可;
(3)易得喜欢①的人数最多,先求出喜欢①的人数所占的比例,然后根据①所占的比例,可得出选择这种方法的大约人数.
解答:解:(1)12÷(90°÷360°)=48(人);
即抽取问卷答案的学生人数为48人;
(2)48×25%=12(人)
即喜欢第②种方法的人数为12人,
补全统计图如下:
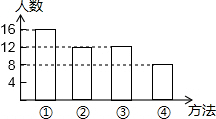 .
.
(3)喜欢①的人数所占的比例=
=
,
喜欢②的人数所占的比例=
,
喜欢③的人数所占的比例=
,
喜欢④的人数所占的比例=
=
,
则全年级同学最喜欢的教学方法是第④种,
选择这种方法的人数=420×
=120人.
喜欢这种方法的人数所占扇形圆心角=360°×
=120°.
即抽取问卷答案的学生人数为48人;
(2)48×25%=12(人)
即喜欢第②种方法的人数为12人,
补全统计图如下:
 .
.(3)喜欢①的人数所占的比例=
| 16 |
| 48 |
| 1 |
| 3 |
喜欢②的人数所占的比例=
| 1 |
| 4 |
喜欢③的人数所占的比例=
| 1 |
| 4 |
喜欢④的人数所占的比例=
| 8 |
| 48 |
| 1 |
| 6 |
则全年级同学最喜欢的教学方法是第④种,
选择这种方法的人数=420×
| 1 |
| 3 |
喜欢这种方法的人数所占扇形圆心角=360°×
| 1 |
| 3 |
点评:本题考查了条形统计图及扇形统计图的知识,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目