Question

数学课上，年轻的刘老师在讲授“轴对称”时，设计了如下四种教学方法：
①教师讲，学生听；
②教师让学生自己做；
③教师引导学生画图，发现规律；
④教师让学生对折纸，观察发现规律，然后画图．
数学教研组长将上述教学方法作为调研内容发到全年级8个班420名同学手中，要求每位同学选出自己最喜欢的一种，他随机抽取了60名学生的调查问卷，统计如图：
（1）请将条形统计图补充完整，并计算扇形统计图中方法③的圆心角．
（2）估计全年级同学中最喜欢的教学方法是哪一种？选择这种教学方法的约有多少人？
（3）假如抽取的60名学生集中在某两个班，这个调查结果还合理吗？为什么？
（4）请你对老师的教学方法提出一条合理化的建议．

Answer 1

分析：（1）由题意可知：喜欢方法②的学生有60-6-18-27=9（人）；求方法③的圆心角应先求所占比值，再乘以360°；
（2）根据条形的高低可判断喜欢方法④的学生最多，人数应该等于总人数乘以喜欢方法④所占的比例；
（3）假如抽取的60名学生集中在某两个班，这个调查结果是不合理的，因为缺乏代表性；
（4）鼓励学生主动参与、加强师生互动等．

解答：解：（1）方法②人数为60-6-18-27=9（人）；方法③的圆心角为360°×

18

60

=108°；
补条形图如图：

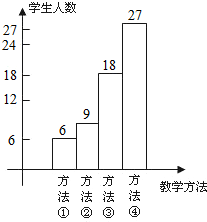
（2）由图可以看出喜欢方法④的学生最多，人数为420×

27

60

=189（人）；
（3）假如抽取的60名学生集中在某两个班，这个调查结果是不合理的，因为缺乏代表性；
（4）如：鼓励学生主动参与、加强师生互动等．

点评：本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．