题目内容
在平行四边形ABCD中，AD：AB=1：2，∠A=60°，AB=4cm，则四边形面积为________．
4
cm2
分析：过点D作DE⊥AB于点E，根据已知可求得AD的长，再根据直角三角形的性质可求得DE的值，然后根据平行四边形的面积公式即可求解．
解答：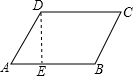
解：如图，过点D作DE⊥AB于点E
∵AD：AB=1：2，AB=4cm
∴AD=2cm
∵DE⊥AB，∠A=60°
∴DE=cm
∴平行四边形的面积=AB•DE=4•=4cm2
故答案为：4cm2．
点评：此题主要考查学生对直角三角形的性质及平行四边形的面积公式的理解及运用能力．
cm2分析：过点D作DE⊥AB于点E，根据已知可求得AD的长，再根据直角三角形的性质可求得DE的值，然后根据平行四边形的面积公式即可求解．
解答：
解：如图，过点D作DE⊥AB于点E∵AD：AB=1：2，AB=4cm
∴AD=2cm
∵DE⊥AB，∠A=60°
∴DE=
cm∴平行四边形的面积=AB•DE=4•
=4cm2故答案为：4
cm2．点评：此题主要考查学生对直角三角形的性质及平行四边形的面积公式的理解及运用能力．
练习册系列答案
相关题目
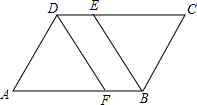如图，在平行四边形ABCD中，∠ABC的平分线交CD于点E，∠ADC的平分线交AB于点F．试判断AF与CE是否相等，并说明理由．
24、已知如图，在平行四边形ABCD中，BN=DM，BE=DF．求证：四边形MENF是平行四边形．
（2013•鞍山一模）在平行四边形ABCD中，∠DAB=60°，点E是AD的中点，点O是AB边上一点，且AO=AE，过点E作直线HF交DC于点H，交BA的延长线于F，以OE所在直线为对称轴，△FEO经轴对称变换后得到△F′EO，直线EF′交直线DC于点M．
如图，在平行四边形ABCD中，AE⊥AD交BD于点E，CF⊥BC交BD于点F．求证：BE=DF．
如图，在平行四边形ABCD中，∠B的平分线交AD于E，AE=10，ED=4，那么平行四边形ABCD的周长是