题目内容
如图, 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片, 为原点,点
为原点,点 在
在 轴的正半轴上,
轴的正半轴上, ,在
,在 上取一点
上取一点 ,将纸片沿
,将纸片沿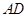 翻折,使点
翻折,使点 落在
落在 边上的点
边上的点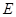 处,求直线
处,求直线 的解析式.
的解析式.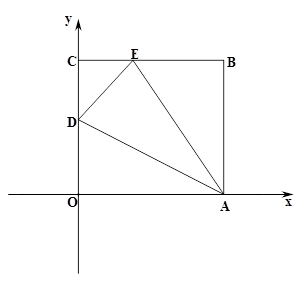
 .
.
解析试题分析:先根据勾股定理求出BE的长,进而可得出CE的长,求出E点坐标,在Rt△DCE中,由DE=OD及勾股定理可求出OD的长,进而得出D点坐标.设出DE所在直线解析式为y=kx+b,把D、E点坐标代入,求出k、b的值即可.
依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=10,AB=8,BE= ,
,
∴CE=4,
∴E(4,8).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD,
∴(8OD)2+42=OD2,
∴OD=5,
∴D(0,5),
设直线 的解析式为
的解析式为 ,
,
则
∴
∴直线 的解析式为
的解析式为 .
.
考点:1.翻折变换(折叠问题);2.一次函数表达式;3.坐标与图形性质.

练习册系列答案
相关题目
某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
| | 甲(kg) | 乙(kg) | 件数(件) |
| A | | 5x | x |
| B | 4(40-x) | | 40-x |
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.
 的图象与反比例函数
的图象与反比例函数 的图象交于一、三象限的A、B两点,与x轴交于点C.已知
的图象交于一、三象限的A、B两点,与x轴交于点C.已知 ,
, ,
, .
. 
 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。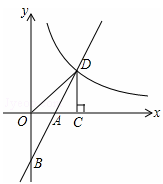





 与
与 相似,若存在,求出点P的坐标,若不存在,请说明理由.
相似,若存在,求出点P的坐标,若不存在,请说明理由.