题目内容
如图，AB∥CD，点E在BC上，且CD=CE，∠D=74°，则∠B的度数为（ ）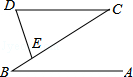
| A．74° | B．32° | C．22° | D．16° |
B．
解析试题分析：根据等腰三角形两底角相等求出∠C的度数，再根据两直线平行，内错角相等解答即可:
∵CD=CE，∴∠D=∠DEC．
∵∠D=74°，∴∠C=180°-74°×2=32°．
∵AB∥CD，∴∠B=∠C=32°．
故选B．
考点：1．平行线的性质；2．等腰三角形的性质．
练习册系列答案
智慧小复习系列答案
相关题目
如图,已知a∥b，小明把三角板的直角顶点放在直线b上.若∠2=40°,则∠1的度数为
| A．40° | B．35° | C．50° | D．45° |
如图，将三角尺的直角顶点放在直尺的一边上，
,
,则
的度数等于（ ）
A． | B． | C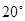． | D． |
如图，AB∥CD，且∠1=20°，∠2=45°＋α，∠3=60°－α，∠4=40°－α，∠5=30°．则α的值为（ ）
| A．10° | B．15° | C．20° | D．25° |
如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3的度数 等于（ ）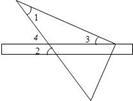
| A．20° | B．50° | C．30° | D．15° |