题目内容
某办公用品销售商店推出两种优惠方式:①购一个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠。书包每个定价20元,水性笔每支定价5元。小丽和同学需要买4个书包,水性笔若干支(不少于4支)。
(1)分别写出两种优惠方式购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;
(2)对x的取值情况进行分析,说明按哪种优惠方式购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济。
(1) ,
,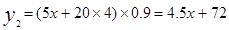
(2)当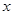 >
>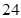 时,选择优惠方法②,当
时,选择优惠方法②,当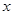 =
=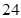 时,选择优惠方法①,②均可。 当
时,选择优惠方法①,②均可。 当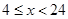 时,选择优惠方法①(3)用优惠方法①购买4个书包,获赠4支水性笔,再用优惠方法②购买8支水性笔
时,选择优惠方法①(3)用优惠方法①购买4个书包,获赠4支水性笔,再用优惠方法②购买8支水性笔
【解析】(1)(3分)设按优惠方法①购买需用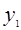 元,按优惠方法②购买需用
元,按优惠方法②购买需用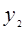 元 1分
元 1分
 2分
2分
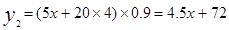 3分
3分
(2)(3分)
设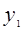 >
>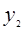 ,即
,即 >
>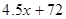
∴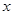 >
>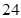 当
当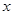 >
>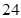 时,选择优惠方法②
4分
时,选择优惠方法②
4分
当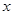 =
=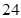 时,选择优惠方法①,②均可。
时,选择优惠方法①,②均可。
当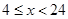 时,选择优惠方法① 6分
时,选择优惠方法① 6分
(3)(3分) 因为需要购买4个书包和12支水性笔,而 <
<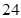 ,
,
所以只用方法②购买不是最经济的。
购买方法一:用优惠方法①购买,需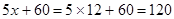 元 7分
元 7分
购买方法二:采用两种购买方式,用优惠方法①购买4个书包,
需要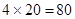 元, 同时获赠4支水性笔;
8分
元, 同时获赠4支水性笔;
8分
再用优惠方法②购买8支水性笔,需要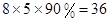 元;
元;
共需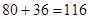 元。显然
元。显然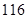 <
<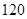
故最佳购买方案是:用优惠方法①购买4个书包,获赠4支水性笔,再用优惠方法②购买8支水性笔 9分
(1)由于①购1个书包,赠送1支水性笔,而需买4个书包,由此得到还要买(x-4)支水性笔,
所以得到y1=(x-4)×5+20×4;又购书包和水性笔一律按9折优惠,所以得到y2=(5x+20×4)×0.9;
(2)设y1>y2,求出当x>24时选择2优惠;当4≤x≤24时,选择1优惠.
(3)分别求出方案一与方案二所用的价钱,再相比较.
