题目内容
某中学库存960套旧课桌椅准备修理。现有甲、乙两个木工小组都想承接这项业务。经协商后得知:甲小组单独修理这批桌椅比乙小组多用20天;乙小组每天比甲小组多修8套;学校每天需付甲小组修理费80元,付乙小组120元。
(1)求甲、乙两个小组每天各修理桌櫈多少套?
(2)在修理过程中,学校要委派一名修理工进行质量监督,并由学校负担他每天的生活补助10元,现有以下三种修理方案供选择:①由甲单独修理;②由乙单独修理;③由甲、乙共同合作修理。你认为哪种方案既省时又省钱?试比较说明。
(1)求甲、乙两个小组每天各修理桌櫈多少套?
(2)在修理过程中,学校要委派一名修理工进行质量监督,并由学校负担他每天的生活补助10元,现有以下三种修理方案供选择:①由甲单独修理;②由乙单独修理;③由甲、乙共同合作修理。你认为哪种方案既省时又省钱?试比较说明。
(1)甲每天修理就课桌椅16套,乙每天修理课桌椅24套;(2)甲乙合作
试题分析:(1)设甲每天修理旧课桌椅x套,则乙每天修理旧课桌椅(x+8)套,根据甲小组单独修理这批桌椅比乙小组多用20天,即可列方程求解;
(2)分别计算出各种方案所需费用,再比较即可判断.
(1)设甲每天修理旧课桌椅x套,则乙每天修理旧课桌椅(x+8)套,由题意得

解得
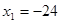 (舍),
(舍),
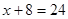 (套)
(套)答:甲每天修理旧课桌椅16套,乙每天修理旧课桌椅24套;
(2)甲单独完成需要960÷16=60天,需要
 元
元乙单独完成需要960÷24=40天,需要
 元
元甲乙合作需要960÷(16+24)=24天,需要
 元
元所以选择甲乙合作完成。
点评:解答本题的关键是读懂题意,找到等量关系,正确列出方程,再求解.

练习册系列答案
相关题目
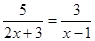
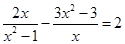 时,若设
时,若设 ,则方程可化为 .
,则方程可化为 . ="2+"
="2+" 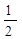 的解为:x1=2;x2=
的解为:x1=2;x2=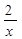 =m+
=m+ 的解为:x1=m;x2=
的解为:x1=m;x2= =m-
=m- 的解为:x1=m;x2= -
的解为:x1=m;x2= - ="b+"
="b+"  的解为:x1=" b" ;x2=
的解为:x1=" b" ;x2= =a+
=a+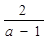
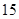 千米到李庄,甲比乙每小时多走
千米到李庄,甲比乙每小时多走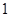 千米,结果比乙早到半小时.问二人每小时各走几千米?
千米,结果比乙早到半小时.问二人每小时各走几千米? 的分式方程是 ( )
的分式方程是 ( )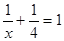 ;
;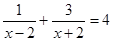 ;
; ;
;


