题目内容
【题目】如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数;
(2)如果AC=![]() ,求DE的长.
,求DE的长.
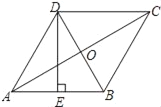
【答案】(1)120°;(2)![]()
【解析】试题分析:(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,再根据菱形的四条边都相等可得AB=AD,然后求出AB=AD=BD,从而得到△ABD是等边三角形,再根据等边三角形的性质求出△DAB=60°,然后根据两直线平行,同旁内角互补求解即可;
(2)根据菱形的对角线互相平分求出AO,再根据等边三角形的性质可得DE=AO.
解:(1)∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∴∠DAB=60°.
∵菱形ABCD的边AD∥BC,
∴∠ABC=180°﹣∠DAB=180°﹣60°=120°,
即∠ABC=120°;
(2)∵四边形ABCD是菱形,
∴BD⊥AC于O,AO=AC=×4=2,
由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=2.

练习册系列答案
相关题目