题目内容
【题目】点A(m,n)为直线y=-x+4上一动点,且满足-4<m<4,将O点绕点B![]() 逆时针旋转90°得点C,连接AC,则线段AC长度的取值范围是____________.
逆时针旋转90°得点C,连接AC,则线段AC长度的取值范围是____________.
【答案】2![]() ≤AC<10
≤AC<10![]() .
.
【解析】
首先证明点A在运动过程中,△ABC的形状相同,推出AB的值最大时,AC的值最大,AB的值最小时,AC的值最小,结合图形分别求出AB的最大值,最小值即可解决问题.
如图1中,

∵A(m,n),
∴点A关于原点对称点A′(-m,-n),
∴OA′的中点B(-![]() ,-
,-![]() );
);
∴OA=2OB=2BC,
∴tan∠CAB=![]() ,
,
∴点A在运动过程中,△ABC的形状相同,
∴AB的值最大时,AC的值最大,AB的值最小时,AC的值最小,
当点A的坐标为(-4,8)时,AB的值最大,
此时B(2,-4),
∴AB=![]() ,
,
∴BC=![]() AB=2
AB=2![]() ,
,
∴AC=![]() .
.
如图2中,当直线AB⊥直线y=-x+4时,AB的值最小,此时直线AB的解析式为y=x,
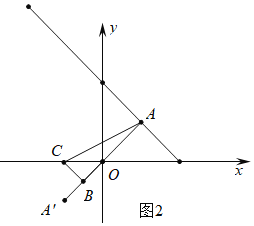
由![]() ,
,
解得![]() ,
,
∴A(2,2),B(-1,-1),
∴AB=![]() ,
,
∴BC=![]() AB=
AB=![]() ,
,
∴AC=![]() ,
,
综上所述,线段AC长度的取值范围是2![]() ≤AC<10
≤AC<10![]() ,
,
故答案为2![]() ≤AC<10
≤AC<10![]() .
.

练习册系列答案
相关题目