题目内容
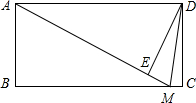 如图所示,在矩形ABCD中,M是BC上一个动点,DE⊥AM,E为垂足,
如图所示,在矩形ABCD中,M是BC上一个动点,DE⊥AM,E为垂足,(1)求证:△ADE∽△ABM;
(2)若3AB=2BC,并且AB,BC的长是方程x2-(k-2)x+2k=0的两个根.求k的值.
考点:相似三角形的判定与性质,根与系数的关系,矩形的性质
专题:
分析:(1)先根据矩形的性质,得到AD∥BC,则∠DAE=∠AMB,又由∠DEA=∠B,根据有两角对应相等的两三角形相似,即可证明出△DAE∽△AMB;
(2)根据根与系数的关系,列出方程组解答即可.
(2)根据根与系数的关系,列出方程组解答即可.
解答:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△ADE∽△ABM;
(2)∵AB,BC的长是方程x2-(k-2)x+2k=0的两个根,
∴
,
∵3AB=2BC,
∴
,
即3k2-37k+12=0,解得k=12或k=
.
∴AD∥BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△ADE∽△ABM;
(2)∵AB,BC的长是方程x2-(k-2)x+2k=0的两个根,
∴
|
∵3AB=2BC,
∴
|
即3k2-37k+12=0,解得k=12或k=
| 1 |
| 3 |
点评:此题主要考查了相似三角形的判定与性质,矩形的性质.(1)中根据矩形的对边平行进而得出∠DAE=∠AMB是解题的关键,此题还将动点问题与一元二次方程和矩形的性质相结合,综合性不错.

练习册系列答案
相关题目
已知
(x≠y),则
+
的值是( )
|
| y |
| x |
| x |
| y |
A、2+2
| ||
B、-2-2
| ||
C、2-
| ||
D、2+
|
下列根式中属于最简二次根式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
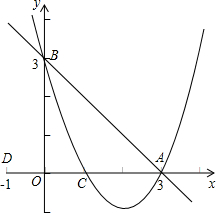 如图已知:直线L1:y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
如图已知:直线L1:y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点. (1)解方程:(x-1)2+2x-3=0
(1)解方程:(x-1)2+2x-3=0