题目内容
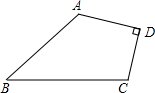 如下图,已知AD⊥CD于D,且AD=4,CD=3,AB=12,BC=13.
如下图,已知AD⊥CD于D,且AD=4,CD=3,AB=12,BC=13.求:(1)四边形ABCD的面积;
(2)若∠B=35°,求∠ACB的度数.
分析:(1)先连接AC,根据勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ABC是直角三角形,然后根据直角三角形的面积公式求解即可.
(2)由(1)可知,△ABC是直角三角形,根据其三边关系可判断出直角三角形的两直角边及斜边,再根据直角三角形中两锐角互余解答即可.
(2)由(1)可知,△ABC是直角三角形,根据其三边关系可判断出直角三角形的两直角边及斜边,再根据直角三角形中两锐角互余解答即可.
解答: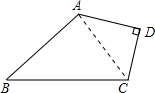 解:(1)连接AC,∵AD⊥CD于D,AD=4,CD=3,
解:(1)连接AC,∵AD⊥CD于D,AD=4,CD=3,
∴AC=
=
=5;
在△ABC中,∵AB=12,BC=13,AC=5,52+122=132,即AC2+AB2=BC2,
∴△ABC是直角三角形,
∴S四边形ABCD=S△ACD+S△ABC
=
AD•CD+
AB•AC
=
×3×4+
×12×5
=6+30
=36.
(2)∵△ABC是直角三角形,AC2+AB2=BC2,∴∠BAC=90°,
∵∠B=35°,∴∠ACB=90°-35°=55°.
 解:(1)连接AC,∵AD⊥CD于D,AD=4,CD=3,
解:(1)连接AC,∵AD⊥CD于D,AD=4,CD=3,∴AC=
| AD2+CD2 |
| 42+32 |
在△ABC中,∵AB=12,BC=13,AC=5,52+122=132,即AC2+AB2=BC2,
∴△ABC是直角三角形,
∴S四边形ABCD=S△ACD+S△ABC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=6+30
=36.
(2)∵△ABC是直角三角形,AC2+AB2=BC2,∴∠BAC=90°,
∵∠B=35°,∴∠ACB=90°-35°=55°.
点评:本题考查勾股定理的逆定理的应用.解答此题的关键是作出辅助线,构造出直角三角形,求出AC的长,再判断出△ABC为直角三角形,再利用三角形的面积公式即可解答.

练习册系列答案
相关题目
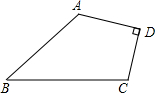 如下图,已知AD⊥CD于D,且AD=4,CD=3,AB=12,BC=13.
如下图,已知AD⊥CD于D,且AD=4,CD=3,AB=12,BC=13.