��Ŀ����
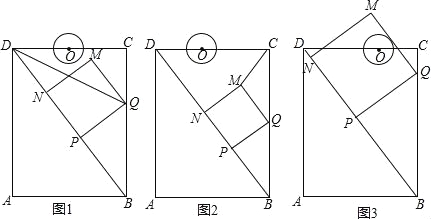
����Ŀ����ͼ���ھ���ABCD�У�AB=6cm��AD=8cm����P�ӵ�B�������ضԽ���BD���D�����˶����ٶ�Ϊ4cm/s������P��PQ��BD��BC�ڵ�Q����PQΪһ����������PQMN��ʹ�õ�N��������PD�ϣ���O�ӵ�D��������DC���C�����˶����ٶ�Ϊ3m/s����OΪԲ�ģ�0.8cmΪ�뾶����O����P���Oͬʱ�����������ǵ��˶�ʱ��Ϊt����λ��s����0��t������
��1����ͼ1������DQƽ�֡�BDCʱ��t��ֵΪ ��
��2����ͼ2������CM������CMQ����CQΪ�ĵ��������Σ���t��ֵ��
��3�������������̽����������������⣺
��֤�������˶������У���Oʼ����QM����ֱ�ߵ���ࣻ
����ͼ3�����˶������У���QM���O����ʱ����t��ֵ�����жϴ�ʱPM���O�Ƿ�Ҳ���У�˵�����ɣ�
���𰸡���1������2������3����֤������������t=��PM����O������.
��������
�����������1����֤��PBQ�ס�CBD�����PQ��BQ�����������tֵ����2����֤��QTM�ס�BCD�������߶γɱ��������tֵ����3����QM��CD��E������DE��DO��ֵ�ȽϿ��жϵ�Oʼ����QM����ֱ�ߵ���ࣻ��������֪��Oֻ���������ֱ��QM�����ڵ�H��QM��CD���ڵ�E������OHE�ס�BCD�������߶γɱ�������tֵ�������÷�֤��֤��ֱ��PM����������O����.
����������⣺��1����ͼ1�У��ھ���ABCD�У���A=��C=��ADC=��ABC=90����AB=CD=6��AD=BC=8����![]() ����PQ��BD�����BPQ=90�����ߡ�PBQ=��DBC����BPQ=��C�����PBQ�ס�CBD����==����==����PQ=3t��BQ=5t����DQƽ����BDC��QP��DB��QC��DC����QP=QC����3t=6��5t��
����PQ��BD�����BPQ=90�����ߡ�PBQ=��DBC����BPQ=��C�����PBQ�ס�CBD����==����==����PQ=3t��BQ=5t����DQƽ����BDC��QP��DB��QC��DC����QP=QC����3t=6��5t��
��t=.��2���⣺��ͼ2�У���MT��BC��T����MC=MQ��MT��CQ����TC=TQ���� TQ=��8��5t����QM=3t��
��MQ��BD�����MQT=��DBC���ߡ�MTQ=��BCD=90�������QTM�ס�BCD����=����
��t=��s������t=sʱ����CMQ����CQΪ�ĵ��������Σ���3����֤������ͼ2�У��ɴ�QM��CD��E��
��EQ��BD����=����EC=��8��5t����ED=DC��EC=6����8��5t��=t����DO=3t����DE��DO=t��3t=t��0������O��ֱ��QM��࣮���⣺��ͼ3�У�������֪��Oֻ���������ֱ��QM�����ڵ�H��QM��CD���ڵ�E����EC=��8��5t����DO=3t����OE=6��3t����8��5t��=t����OH��MQ�����OHE=90�����ߡ�HEO=��CEQ��
���HOE=��CQE=��CBD���ߡ�OHE=��C=90�������OHE�ס�BCD����=���� ����t=��
����t=��
��t=sʱ����O��ֱ��QM���У�����PM������PM����O���У�����OMH= PMQ=22.5������MH��ȡһ��F��ʹ��MF=FO������FMO=��FOM=22.5�������OFH=��FOH=45������OH=FH=0.8��FO=FM=0.8 ����MH=0.8��+1����
��=�õ�HE=����=�õ�EQ=����MH=MQ��HE��EQ=4- - =��
��0.8��+1������ì�ܣ������費��������ֱ��MQ����O�����У�




 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д�