题目内容
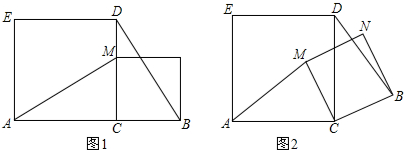
如图1,点C在线段AB上,分别以AC、BC为边在线段AB的同侧作正方形ACDE和BCMN,连结AM、BD.
(1)AM与BD有怎样的关系?为什么?
(2)如果将正方形BCMN绕点C逆时针旋转锐角α,其它不变(如图2).(1)中所得的结论是否仍
然成立?并说明理由.
(1)AM与BD有怎样的关系?为什么?
(2)如果将正方形BCMN绕点C逆时针旋转锐角α,其它不变(如图2).(1)中所得的结论是否仍
然成立?并说明理由.

分析:(1)利用正方形的性质和已知条件证明△AMC≌△DBC,从而求出AM=BD;
(2)如果将正方形BCMN绕点C逆时针旋转锐角α,其它不变(1)中所得的结论任然成立,先求出∠ACM=∠DCB,然后利用“边角边”证明△AMC和△DBC全等,再根据全等三角形对应边相等即可得证.
(2)如果将正方形BCMN绕点C逆时针旋转锐角α,其它不变(1)中所得的结论任然成立,先求出∠ACM=∠DCB,然后利用“边角边”证明△AMC和△DBC全等,再根据全等三角形对应边相等即可得证.
解答:(1)∵四边形ACDE和四边形BCMN都为正方形,
∴AC=DC,∠ACD=∠BCD=90°,BC=CM,
在△AFC和△DBC中,
,
∴△AMC≌△DBC(SAS).
∴AM=BD;
(2)如果将正方形BCMN绕点C逆时针旋转锐角α,其它不变(1)中所得的结论任然成立,
理由如下:
AM=BD仍然成立.
理由如下:在正方形ABCE和正方形BCMN中,AB=CD,CM=BC,∠ACD=∠DCB=90°,
∵∠ACM=90°-∠MCD,
∠DCB=90°-∠MCD,
∴∠ACM=∠CDCB,
在△ACM和△DCB中,
,
∴∴△AMC≌△DBC(SAS).
∴AM=BD.
∴AC=DC,∠ACD=∠BCD=90°,BC=CM,
在△AFC和△DBC中,
|
∴△AMC≌△DBC(SAS).
∴AM=BD;
(2)如果将正方形BCMN绕点C逆时针旋转锐角α,其它不变(1)中所得的结论任然成立,
理由如下:
AM=BD仍然成立.
理由如下:在正方形ABCE和正方形BCMN中,AB=CD,CM=BC,∠ACD=∠DCB=90°,
∵∠ACM=90°-∠MCD,

∠DCB=90°-∠MCD,
∴∠ACM=∠CDCB,
在△ACM和△DCB中,
|
∴∴△AMC≌△DBC(SAS).
∴AM=BD.
点评:本题考查了正方形的性质,全等三角形的判定与性质以及旋转等知识,熟练利用正方形的性质得出是解题的关键.

练习册系列答案
相关题目

 (2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,
(2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,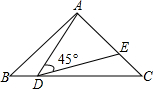 在Rt△ABC中,∠BAC=90°,AB=AC=10,点D在BC所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).如图,若点D在线段BC上运动,DE交AC于E.
在Rt△ABC中,∠BAC=90°,AB=AC=10,点D在BC所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).如图,若点D在线段BC上运动,DE交AC于E.