题目内容
 根据下列推理过程填空,并在括号内加注理由.
根据下列推理过程填空,并在括号内加注理由.
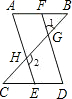
已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(________).
∵∠1+∠2=180°(________).
∴∠CGD+∠2=180°(________).
∴AE∥FD(________).
∴∠A=∠BFD(________).
又∵∠A=∠D(________).
∴∠BFD=∠D(________).
∴AB∥CD(________).
对顶角相等 已知 等量代换 同旁内角互补,两直线平行 两直线平行,同位角相等 已知 等量代换 内错角相等,两直线平行
分析:围绕证题思路,结合图形,利用平行线的性质及判定逐步分析解答.
解答:证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(对顶角相等).
∵∠1+∠2=180°(已知).
∴∠CGD+∠2=180°(等量代换).
∴AE∥FD(同旁内角互补,两直线平行).
∴∠A=∠BFD(两直线平行,同位角相等).
又∵∠A=∠D(已知).
∴∠BFD=∠D(等量代换).
∴AB∥CD(内错角相等,两直线平行).
点评:本题利用了平行线的判定和性质,还利用了对顶角相等,等量代换等知识.
分析:围绕证题思路,结合图形,利用平行线的性质及判定逐步分析解答.
解答:证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(对顶角相等).
∵∠1+∠2=180°(已知).
∴∠CGD+∠2=180°(等量代换).
∴AE∥FD(同旁内角互补,两直线平行).
∴∠A=∠BFD(两直线平行,同位角相等).
又∵∠A=∠D(已知).
∴∠BFD=∠D(等量代换).
∴AB∥CD(内错角相等,两直线平行).
点评:本题利用了平行线的判定和性质,还利用了对顶角相等,等量代换等知识.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
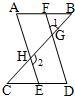 14、根据下列推理过程填空,并在括号内加注理由.
14、根据下列推理过程填空,并在括号内加注理由.