题目内容
当1＜x＜2时，化简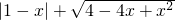
的结果是
- A.-1
- B.2x-1
- C.1
- D.3-2x
C
分析：先将4-4x+x2整理成（x-2）2的形式，再根据二次根式的性质解答．
解答：∵1＜x＜2，
∴1-x＜0，x-2＜0，
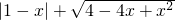∴=|1-x|
=|1-x|+|2-x|
=（x-1）+（2-x）=1．
故选C．
点评：解答此题，要弄清以下问题：
①定义：一般地，形如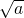
（a≥0）的代数式叫做二次根式．当a＞0时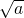，表示a的算术平方根；当a=0时，
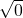=0；当a＜0时，二次根式无意义．
②性质：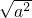
=|a|．
分析：先将4-4x+x2整理成（x-2）2的形式，再根据二次根式的性质解答．
解答：∵1＜x＜2，
∴1-x＜0，x-2＜0，
∴
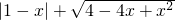=|1-x|=|1-x|+|2-x|
=（x-1）+（2-x）=1．
故选C．
点评：解答此题，要弄清以下问题：
①定义：一般地，形如
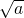（a≥0）的代数式叫做二次根式．当a＞0时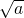，表示a的算术平方根；当a=0时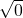，=0；当a＜0时，二次根式无意义．②性质：
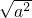=|a|． 
练习册系列答案
相关题目
当1＜x＜3时，化简
+
的结果是（ ）
| (x-3)2 |
| (1-x)2 |
| A、4-2x | B、2 |
| C、2x-4 | D、4 |