题目内容
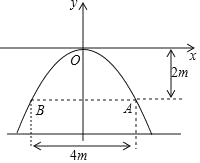
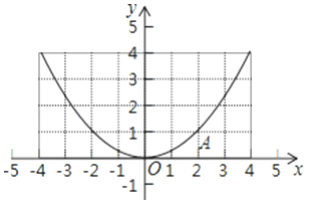
【题目】如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),
(1)求出二次函数的表达式;
(2)我们把横、纵坐标都为整数的点称为整点,请用整数n表示这条抛物线上所有的整点坐标.
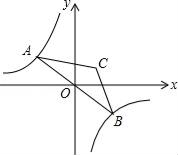
(3)过y轴的正半轴上一点C(0,a)作AO的平行线交抛物线于点B,
①求出直线BC的函数表达式(用a表示);
②如果点B是整点,求证:△OAB的面积是偶数.
【答案】(1)y=![]() x2;(2)抛物线上整点坐标可表示为(2n,n2),其中n为整数;(3)①y=
x2;(2)抛物线上整点坐标可表示为(2n,n2),其中n为整数;(3)①y=![]() x+a;②详见解析.
x+a;②详见解析.
【解析】
(1)可设抛物线的解析式为y=ax2,然后只需把点A的坐标代入抛物线的解析式,就可解决问题;
(2)由抛物线的解析式可知,要使y是整数,只需x是偶数,故x可用2n表示(n为整数),由此就可解决问题;
(3)①可运用待定系数法求出直线OA的解析式,然后根据两直线平行一次项的系数相同,就可得到直线BC的函数表达式;②由于点B是整点,点B的坐标可表示为(2n,n2),代入直线BC的解析式,即可得到a的值(用n表示),然后根据平行等积法可得S△OAB=S△OAC=n(n-1),由于n与n-1是相邻整数,必然一奇一偶,因而n(n-1)是偶数,问题得以解决.
(1)设抛物线的解析式为y=ax2,
把A(2,1)代入y=ax2,得1=4a,
解得a=![]() ,
,
∴二次函数的表达式为y=![]() x2;
x2;
(2)抛物线上整点坐标可表示为(2n,n2),其中n为整数;
(3)①设直线OA的解析式为y=kx,
把点A(2,1)代入y=kx,得1=2k,
解得k=![]() ,
,
∴直线OA的解析式为y=![]() x,
x,
则过点C(0,a)与直线OA平行的直线的解析式为y=![]() x+a;
x+a;
②证明:∵点B是整点,
∴点B的坐标可表示为(2n,n2),其中n为整数,
把B(2n,n2)代入y=![]() x+c,得n2=n+c,
x+c,得n2=n+c,
∴c=n2﹣n=n(n﹣1).
∵BC∥OA,
∴S△OAB=S△OAC=![]() ×c×2=c=n(n﹣1).
×c×2=c=n(n﹣1).
∵n为整数,
∴n与n﹣1一奇一偶,
∴n(n﹣1)是偶数,
∴△OAB的面积是偶数.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案