题目内容
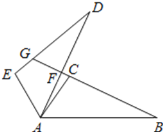
【题目】如图,点A在直线l上,△ABC与△AB′C′关于直线l对称,连接BB′分别交AC,AC′于点D′,连接CC′,下列结论不一定正确的是( )
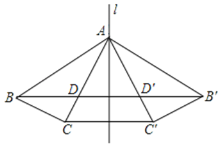
A.∠BAC=∠B′AC′B.CC′∥BB′C.BD=B′D′D.AD=DD′
【答案】D
【解析】
根据对称性易证△ABD≌△AB′D′,再根据对应角相等对应边相等,AC正确;由全等得出AD=AD′,则∠ADD′=(180°-∠A)÷2,由题意AC=AC′,∠ACC′=(180°-∠A)÷2,即可证B正确.
∵△ABC与△AB′C′关于直线l对称.
∴∠BAC=∠B′AC′,A选项正确.
由条件可得:AB=AB′,则∠ABD=∠AB′D′.
在△ABD和△AB′D′中
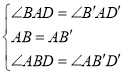
△ABD≌△AB′D′(SAS)
∴BD=B′D′,C选项正确.
∴AD=AD′,则∠ADD′=(180°-∠A)÷2,
又∵由题意得AC=AC′,则∠ACC′=(180°-∠A)÷2
∴∠ADD′=∠ACC′
∴CC′∥BB′,B选项正确
故选D

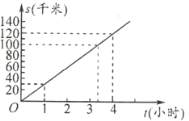
【题目】近年来“哈罗单车”和“哈啰助力车”在街头流行.随着市民对这两种车的使用率的提升,经营“哈罗单车”和“哈啰助力车”的两家公司也有了越来越高的收人.初三某班的实践小组对两家公司近10个周的收入进行了调查,就收入(单位:千元)情况制作了如下的统计图:

根据以上信息,整理分析数据如下:
公司 | 平均周收入/千元 | 周收入中位数/千元 | 周收入众数/千元 | 方差 |
哈罗单车 | _____ | 6 | 6 | 1.2 |
哈啰助力车 | 6 | _____ | 4 | _____ |
(1)完成表格填空;
(2)“哈罗单车”和“哈啰助力车”在该地各有500辆和300辆.从收入的情况看,上个周这2家公司都达到了近10个周的最高收人.已知每骑用一次“哈罗单车”和“哈啰助力车”,公司就分别收人1元和2元,通过计算在上周每辆车的周平均骑用次数,说明哪种车比较抢手?