题目内容
等腰梯形的高是4，对角线与下底的夹角是45°，则该梯形的中位线是
- A.4
- B.6
- C.8
- D.10
A
分析：由等腰梯形的高是4，对角线与下底的夹角是45°，可以得到上底+下底，中位线=
×（上底+下底），则可得到结果．
解答：
解：如图所示：
BG为高，EF为中位线，
AB平行CD，AB是上底
BG⊥CD，AH⊥CD
∵BG⊥CD
∠BCG=45°，
则CG=4
又∵AH⊥CD
∠ADH=45°，
所以DH=4．
又DH+CG=CH+DG+HG+HG=CD+HG
其中HG=AB
所以AB+CD=CD+HG=DH+CG=8
所以中位线=
=
=4．
故选（A）．
点评：本题考查的知识比较全面，需要用到梯形和三角形中位线定理以及直角三角形的性质．
分析：由等腰梯形的高是4，对角线与下底的夹角是45°，可以得到上底+下底，中位线=
×（上底+下底），则可得到结果．解答：
解：如图所示：BG为高，EF为中位线，
AB平行CD，AB是上底
BG⊥CD，AH⊥CD
∵BG⊥CD
∠BCG=45°，
则CG=4
又∵AH⊥CD
∠ADH=45°，
所以DH=4．
又DH+CG=CH+DG+HG+HG=CD+HG
其中HG=AB
所以AB+CD=CD+HG=DH+CG=8
所以中位线=
==4．故选（A）．
点评：本题考查的知识比较全面，需要用到梯形和三角形中位线定理以及直角三角形的性质．
练习册系列答案
相关题目
下列命题正确的是：①对角线互相垂直且相等的平行四边形是正方形；②平行四边形、矩形、等边三角形、正方形既是中心对称图形，也是轴对称图形；③旋转和平移都不改变图形的形状和大小；④底角是45°的等腰梯形，高是h，则腰长是
h．（ ）
| 2 |
| A、全对 | B、①②④ |
| C、①②③ | D、①③④ |
．（ ）
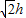