题目内容
【题目】中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形!
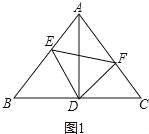
(1)如图1,若点D为等腰直角三角形ABC斜边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°,连接AD、EF,当BC=5![]() ,FC=2时,求EF的长度;
,FC=2时,求EF的长度;
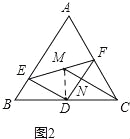
(2)如图2,若点D为等边三角形ABC边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°;M为EF的中点,连接CM,当DF∥AB时,证明:3ED=2MC;
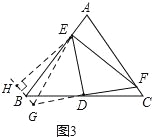
(3)如图3,若点D为等边三角形ABC边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°;当BE=6,CF=0.8时,直接写出EF的长度.

【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
试题分析:(1)根据等腰直角三角形的性质,证得△ADE≌△CDF,根据全等三角形对应边相等,求得AE=CF=2,最后在在Rt△AEF中根据勾股定理求得EF的长;
(2)先设等边三角形边长为2,在Rt△BDE中求得DE的长,再根据CM垂直平分DF,在Rt△CDN中求得CN,在Rt△MND中求得MN的长,最后根据CM与DE的长度之比求得3ED=2MC;
(3)先延长FD至G,使得FD=FG,连接EG,BG,过E作EH⊥BG于点H,根据△BDG≌△CDF得到BG=CF=0.8,进而在Rt△BEH中求得HE,在Rt△EHG中求得EG,最后根据ED垂直平分FG,即可得出EF的长度.
试题解析:(1)如图1∵点D为等腰直角三角形ABC斜边BC的中点
∴AD⊥BC,AD=![]() BC=CD=
BC=CD=![]() ,∠DAE=∠C=45°,∴AC=
,∠DAE=∠C=45°,∴AC=![]() CD=5,又∵∠EDF=90°,FC=2
CD=5,又∵∠EDF=90°,FC=2
∴∠ADE=∠CDF,AF=5﹣2=3
在△ADE和△CDF中
∴△ADE≌△CDF(ASA),∴AE=CF=2,∴在Rt△AEF中,EF=![]() =
=![]()
(2)设等边三角形边长为2,则BD=CD=1,
∵等边三角形ABC中,DF∥AB
∴∠FDC=∠B=60°
∵∠EDF=90°
∴∠BDE=30°
∴DE⊥BE
∴BE=![]() ,DE=
,DE=![]()
如图2,连接DM,则Rt△DEF中,DM=![]() EF=FM
EF=FM
∵∠FDC=∠FCD=60°
∴△CDF是等边三角形
∴CD=CF=1
∴CM垂直平分DF
∴∠DCN=30°
∴Rt△CDN中,DN=![]() ,CN=
,CN=![]() ,DF=1
,DF=1
∴在Rt△DEF中,EF= =
=![]()
∵M为EF的中点
∴FM=DM=![]()
∴Rt△MND中,MN=
∴CM=![]() +
+![]() =
=![]()
∴![]() =
=![]() =
=![]()
∴3ED=2MC
(3)如图3,延长FD至G,使得FD=DG,连接EG,BG,则ED垂直平分FG,故EF=EG
∴由BD=CD,∠BDG=∠CDF,DF=DG可得:△BDG≌△CDF
∴∠GBD=∠C=60°,BG=CF=0.8
∴∠EBG=60°+60°=120°
∴∠EBH=60°
过E作EH⊥BG于点H,则BH=![]() BE=3
BE=3
∴Rt△BEH中,HE=![]() =
=![]()
∴Rt△EHG中,EG=![]() =
=![]()
∴EF的长度为![]()

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案