题目内容
【题目】如图,直线y=2x+m(m>0)与x轴交于点A(﹣2,0),直线y=﹣x+n(n>0)与x轴、y轴分别交于B,C两点,并与直线y=2x+m(m>0)相交于点D,若AB=4. 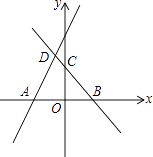
(1)求点D的坐标;
(2)求出四边形AOCD的面积;
(3)若E为x轴上一点,且△ACE为等腰三角形,求点E的坐标.
【答案】
(1)解:把A(﹣2,0)代入y=2x+m得﹣4+m=0,解得m=4,
∴y=﹣2x+4,
∵AB=4,A(﹣2,0),
∴B点坐标为(2,0),
把B(2,0)代入y=﹣x+n得﹣2+n=0,解得n=2,
∴y=﹣x+2,
解方程组 ![]() 得
得 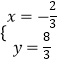 ,
,
∴D点坐标为(﹣ ![]() ,
, ![]() )
)
(2)解:当x=0时,y=﹣x+2=2,
∴C点坐标为(0,2),
∴四边形AOCD的面积=S△DAB﹣S△COB
= ![]() ×4×
×4× ![]() ﹣
﹣ ![]() ×2×2
×2×2
= ![]()
(3)解:∵A(﹣2,0),C(0,2),
∴AC=2 ![]() ,
,
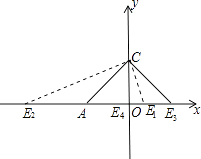
当AE=AC=2 ![]() 时,E1点的坐标为(2
时,E1点的坐标为(2 ![]() ﹣2,0),E2点的坐标为(﹣2
﹣2,0),E2点的坐标为(﹣2 ![]() ﹣2,0);
﹣2,0);
当CE=CA时,E3点的坐标为(2,0),
当EA=EC时,E4点的坐标为(0,0),
综上所述,点E的坐标为(2 ![]() ﹣2,0)、(﹣2
﹣2,0)、(﹣2 ![]() ﹣2,0)、(2,0)、(0,0).
﹣2,0)、(2,0)、(0,0).
【解析】(1)先把A点坐标代入y=2x+m得到m=4,则y=﹣2x+4,再利用AB=4可得到B点坐标为(2,0),则把B点坐标代入y=﹣x+n可得到n=2,则y=﹣x+2,然后根据两直线相交的问题,通过解方程组 ![]() 得到D点坐标;(2)先确定C点坐标为(0,2),然后利用四边形AOCD的面积=S△DAB﹣S△COB进行计算即可;(3)先利用A、C两点的坐标特征得到△ACO为等腰直角三角形,AC=2
得到D点坐标;(2)先确定C点坐标为(0,2),然后利用四边形AOCD的面积=S△DAB﹣S△COB进行计算即可;(3)先利用A、C两点的坐标特征得到△ACO为等腰直角三角形,AC=2 ![]() ,然后分类讨论:当AE=AC=2
,然后分类讨论:当AE=AC=2 ![]() 时,以A点为圆心,2
时,以A点为圆心,2 ![]() 画弧交x轴于E1点和E2点,再写出它们的坐标;当CE=CA时,E3点与点A关于y轴对称,即可得到它的坐标;当EA=EC时,E4点为坐标原点.
画弧交x轴于E1点和E2点,再写出它们的坐标;当CE=CA时,E3点与点A关于y轴对称,即可得到它的坐标;当EA=EC时,E4点为坐标原点.