题目内容
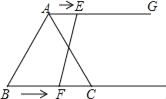
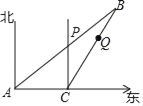
【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿某一方向直航140海里的海岛B,其速度为14海里/小时;乙船速度为20海里/小时,先沿正东方向航行3小时后,到达C港口接旅客,停留1小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
(1)求海岛B到航线AC的距离;
(2)甲船在航行至P处,发现乙船在其正东方向的Q处,问此时两船相距多少?
【答案】(1)海岛B到航线AC的距离为50![]() 海里;(2)两船相距12海里.
海里;(2)两船相距12海里.
【解析】
(1)过点B作BD⊥AE于D,在Rt△BCD中,∠BCD=60°,设CD=x,可得BD=![]() x,在Rt△BDA中,根据勾股定理可得方程1402=(60+x)2+(
x,在Rt△BDA中,根据勾股定理可得方程1402=(60+x)2+(![]() x)2,解方程求得x的值,即可求得BD的长;(2)设运动时间为t,则AP=14t,CQ=20(t﹣4),BC=100,由题意可知PQ∥AC,由平行线分线段成比例定理可得
x)2,解方程求得x的值,即可求得BD的长;(2)设运动时间为t,则AP=14t,CQ=20(t﹣4),BC=100,由题意可知PQ∥AC,由平行线分线段成比例定理可得![]() ,代入数值求得t值,即可求得AP、PB的长;再由△BPQ∽△BAC,根据相似三角形的性质可得
,代入数值求得t值,即可求得AP、PB的长;再由△BPQ∽△BAC,根据相似三角形的性质可得![]() ,代入数据即可求得PQ的长.
,代入数据即可求得PQ的长.
(1)过点B作BD⊥AE于D,
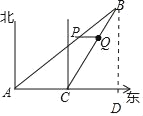
由题意可知AC=60,AB=140,
在Rt△BCD中,∠BCD=60°,
设CD=x,则BD=![]() x,
x,
∵在Rt△BDA中,∠BDA=90°
∴AD2+BD2=AB2,得1402=(60+x)2+(![]() x)2
x)2
x2+30x﹣4000=0,
∴x=50或﹣80(舍弃),
∴BD=50![]() .
.
∴海岛B到航线AC的距离为50![]() 海里;
海里;
(2)设运动时间为t,则AP=14t,CQ=20(t﹣4),BC=100,
若点Q在点P的正东方向,则PQ∥AC,
∴![]() =
=![]() ,即:
,即:![]() =
=![]() ,得t=8,
,得t=8,
∴AP=112,PB=140-112=28.
由∵△BPQ∽△BAC,
∴![]() =
=![]() ,即:
,即:![]() =
=![]() ,
,
得PQ=12.
∴两船相距12海里.

 智慧小复习系列答案
智慧小复习系列答案【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.

【题目】新课程改革十分关注学生的社会实践活动,小明在一次社会实践活动中负责了解他所居住的小区500户居民的家庭月人均收入情况,他从中随机调查了40户居民家庭的“家庭月人均收入情况”(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).
分组 | 频数 | 占比 |
1000≤x<2000 | 3 | 7.5% |
2000≤x<3000 | 5 | 12.5% |
3000≤x<4000 | a | 30% |
4000≤x<5000 | 8 | 20% |
5000≤x<6000 | b | c |
6000≤x<7000 | 4 | 10% |
合计 | 40 | 100% |
(1)频数分布表中,a= ,b= ,C= ,请根据题中已有信息补全频数分布直方图;
(2)观察已绘制的频数分布直方图,可以看出组距是 ,这个组距选择得 (填“好”或“不好”),并请说明理由.
(3)如果家庭人均月收入“大于3000元不足6000元”的为中等收入家庭,则用样本估计总体中的中等收入家庭大约有 户.