Question

如图，已知直线y=x+8交x轴于A点，交y轴于B点，过A、0两点的抛物线y=ax²+bx（a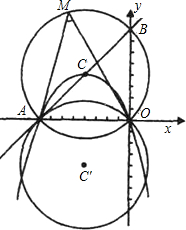＜O）的顶点C在直线AB上，以C为圆心，CA的长为半径作⊙C．
（1）求抛物线的对称轴、顶点坐标及解析式；
（2）将⊙C沿x轴翻折后，得到⊙C′，求证：直线AC是⊙C′的切线；
（3）若M点是⊙C的优弧

ABO

（不与0、A重合）上的一个动点，P是抛物线上的点，且∠POA=∠AM0，求满足条件的P点的坐标．

Answer 1

分析：（1）根据抛物线过A（-8，0），B（0，0）两点可求出其对称轴方程，得C点的横坐标，再根据C点在直线y=x+8上，可求出C点的坐标，即抛物线的顶点坐标．用待定系数法即可求出抛物线的解析式；
（2）连接CC′、C′A，C、C′关于x轴对称，根据对称的性质可知x轴是线段CC′的垂直平分线，故△ACC'是等腰三角形，因为点C（-4，4），所以∠CAO=45°，根据等腰三角形的性质可知∠CAC′=2∠CAO=90°，AC过⊙C′的半径C′A的外端点A，根据切线的定义可知直线AC是⊙C，的切线；
（3）根据C点坐标可知∠ABO=45°，由圆周角可得∠AMO=∠ABO=45°，
设P（x，y）当|

x

y

|=1，即y=x或y=-x时∠POA=45°，故应分y=x，y=-x时两种情况分别代入原函数解析式求出P点坐标．

解答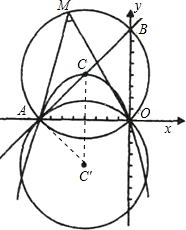：解：（1）如图，由直线y=x+8图象上点的坐标特征可知，A（-8，0），B（0，8）
∵抛物线过A、O两点
∴抛物线的对称点为x=-4
又∵抛物线的对称点在直线AB上，
∴当x=-4时，y=4
∴抛物线的顶点C（-4，4）

4=16a-4b 0=64a-8b

，
解得

a=- 1 4 b=-2

∴抛物线的解析式为y=-

1

4

x²-2x；

（2）连接CC′、C′A
∵C、C′关于x轴对称，设CC′交x轴于D，则CD⊥x轴，且CD=4，AD=4
△ACD为等腰直角三角形
∴△AC′D也为等腰直角三角形
∴∠CAC′=90°
∵AC过⊙C′的半径C′A的外端点A
∴AC是⊙C′的切线；

（3）∵M点是⊙O的优弧

ABO

上的一点，
∴∠AMO=∠ABO=45°，
∴∠POA=∠AMO=45°
当P点在x轴上方的抛物线上时，
设P（x，y），则y=-x，
又∵y=-

1

4

x²-2x
∴

y=-x y=- 1 4 x2-2x

解得

x1=0 y1=0

x2=-4 y2=4

此时P点坐标为（-4，4）当P点在x轴下方的抛物线时，设P（x，y）
则y=x，又∵y=-

1

4

x2-2x
∴

y=x y=- 1 4 x2-2x

解得

x1=0 y1=0

x2=-12 y2=-12

此时P点的坐标为（-12，-12）
综上所述，满足条件的P点坐标为（-4，4）或（-12，-12）

点评：本题综合考查了一次函数、二次函数图象上点的坐标特点及圆的相关知识，比较复杂，但难度适中．