题目内容
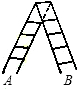 如图是一家用梯子,已知梯子的长度为a,梯子与地面所成的角为78°,那么梯子两脚张开的宽度AB为
如图是一家用梯子,已知梯子的长度为a,梯子与地面所成的角为78°,那么梯子两脚张开的宽度AB为
- A.asin78°
- B.acos78°
- C.atan39°
- D.2acos78°
B
分析:设梯子的顶端是C,则△ABC是等腰三角形,根据三线合一性质,作高线CD,则AB=2BD.在直角△CDB中,利用三角函数即可求解.
解答: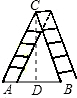 解:
解:
作CD⊥AB,在直角△BCD中,∠CBD=78°,BC= a,cos∠CBD=
a,cos∠CBD= .
.
∴BD=BC•cos∠CBD= a•cos∠CBD=
a•cos∠CBD= a•cos78°,
a•cos78°,
∴AB=2BD=a•cos78°.
故选B.
点评:等腰三角形的计算可以通过作高线,转化为解直角三角形来解决.
分析:设梯子的顶端是C,则△ABC是等腰三角形,根据三线合一性质,作高线CD,则AB=2BD.在直角△CDB中,利用三角函数即可求解.
解答:
 解:
解:作CD⊥AB,在直角△BCD中,∠CBD=78°,BC=
 a,cos∠CBD=
a,cos∠CBD= .
.∴BD=BC•cos∠CBD=
 a•cos∠CBD=
a•cos∠CBD= a•cos78°,
a•cos78°,∴AB=2BD=a•cos78°.
故选B.
点评:等腰三角形的计算可以通过作高线,转化为解直角三角形来解决.

练习册系列答案
相关题目
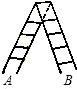 如图是一家用梯子,已知梯子的长度为a,梯子与地面所成的角为78°,那么梯子两脚张开的宽度AB为( )
如图是一家用梯子,已知梯子的长度为a,梯子与地面所成的角为78°,那么梯子两脚张开的宽度AB为( )| A、asin78° | B、acos78° | C、atan39° | D、2acos78° |