题目内容
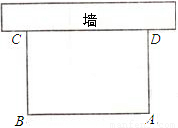
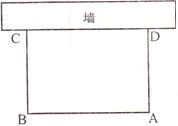 21、如图,利用一面10m长的墙,用20m长的篱笆,围成一个面积为48m2的矩形场地,求这个矩形的长、宽.
21、如图,利用一面10m长的墙,用20m长的篱笆,围成一个面积为48m2的矩形场地,求这个矩形的长、宽.分析:本题可设垂直于墙的边长xm,则平行于墙的边长(20-2x)m,然后利用围成的场地的面积公式即可列出方程,进而求解.
解答:解:设垂直于墙的边长xm,
当场地面积为48m2时,
有x(20-2x)=48,
即x2-10x+24=0,
∴x1=4,x2=6.
∵x=4时,20-2x=12>10,所以x=4不合题意,应舍去.
∴x=6时,20-2x=8.
∴这个矩形的长8m、宽6m.
当场地面积为48m2时,
有x(20-2x)=48,
即x2-10x+24=0,
∴x1=4,x2=6.
∵x=4时,20-2x=12>10,所以x=4不合题意,应舍去.
∴x=6时,20-2x=8.
∴这个矩形的长8m、宽6m.
点评:本题考查了一元二次方程的应用,要仔细分析题意,正确设定未知数列出方程即可解决问题,但应注意解的合理性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
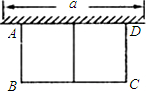 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求: 篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.
篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.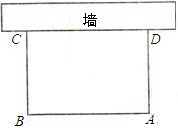 如图,利用一面10m长的墙,用20m长的篱笆,围成一个面积为48m2的矩形场地,求这个矩形的长、宽.
如图,利用一面10m长的墙,用20m长的篱笆,围成一个面积为48m2的矩形场地,求这个矩形的长、宽.